Cho △ABC vuông cân tại A. chứng miinh với mọi M thuộc cạnh huyền BC ta luôn có:
MB2+MC2=2MA2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ML
6 tháng 8 2016
Lấy thêm trung điểm K của BC rồi dùng định lý Pytago tính các cạnh MB, MC, MA theo AB, AC, BC, AK
CH
Cô Hoàng Huyền
Admin
VIP
7 tháng 2 2018
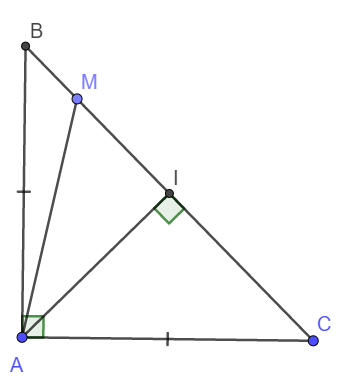
Đặt AB = AC = a \(\Rightarrow BC=\sqrt{AB^2+AC^2}=a\sqrt{2}\)
Gọi I là trung điểm BC, do tam giác ABC cân nên AI cũng là đường cao.
\(AI=BI=IC=\frac{a\sqrt{2}}{2}\)
Đặt MI = x ( 0 < x < \(\frac{a\sqrt{2}}{2}\) )
Ta có \(BM^2=\left(BI-MI\right)^2=\left(\frac{a\sqrt{2}}{2}-x\right)^2\)
\(MC^2=\left(IC+MI\right)^2=\left(\frac{a\sqrt{2}}{2}+x\right)^2\)
\(\Rightarrow MB^2+MC^2=2\left(\frac{a^2}{2}+x^2\right)=2\left(AI^2+MI^2\right)\)
\(=2AM^2\)
Vậy nên ta đã chứng minh được \(\forall M\in BC:BM^2+MC^2=2AM^2\)
17 tháng 9 2023
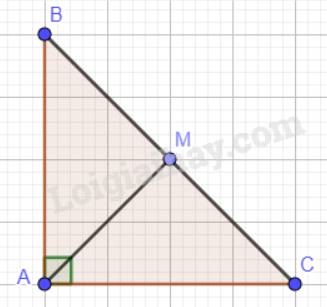
Tam giác ABC vuông cân tại A nên \(\widehat A = 90^\circ ;\widehat B = \widehat C; AB = AC\).
Tổng ba góc trong một tam giác bằng 180° nên \(\widehat B = \widehat C = 90:2 = 45^\circ \).
Xét tam giác ABM và tam giác ACM có:
AB = AC
AM chung
BM = CM
\(\Rightarrow \Delta ABM = \Delta ACM\) (c.c.c)
\(\Rightarrow \widehat {BAM} = \widehat {CAM}\) (2 góc tương ứng)
Mà \(\widehat {BAM} + \widehat {CAM}=\widehat{BAC}=90^0\)
\(\Rightarrow \widehat {BAM} = \widehat {CAM} = 90:2 = 45^\circ \).
Xét tam giác MAB: \(\widehat {MBA} = \widehat {BAM} = 45^\circ \Rightarrow \widehat {BMA} = 90^\circ ;MB = MA\).
Vậy tam giác MAB vuông cân tại M.
BT
9 tháng 11 2017
a) Các tam giác DBA và tam giác EAC vuông cân nên \(\widehat{ABD}=\widehat{DAB}=45^o,\widehat{CAE}=\widehat{ECA}=45^o\).
\(\widehat{DAE}=\widehat{DAB}+\widehat{BAC}+\widehat{CAE}=45^o+90^o+45^o=180^o\).
Suy ra D, A, E thẳng hàng.
b) Có M là trung điểm của BC và tam giác BAC vuông tại A nên MA = MB = MC.
Suy ra \(\Delta DBM=\Delta DAM\left(c.c.c\right)\). Vì vậy \(\widehat{BDM}=\widehat{ADM}\) hay DM là tia phân giác góc ADB.
mà tam giác BDA cân tại D nên DM cũng là đường cao hay \(DM\perp AB\).
Tương tự cho \(EM\perp AC\).
c) Theo chứng minh trên DM là tia phân giá góc ADB nên \(\widehat{BDM}=\widehat{MDA}=45^o\). Tương tự \(\widehat{AEK}=\widehat{KEC}=45^o\).
Vì vậy ta, giác DME vuông cân.
d) Do các tam giác ADB và tam giác AEC cân và DF và EK là đường cao tương ứng nên DF và EK cũng là các đường trung tuyến.
Vì vậy F và K lần lượt là trung điểm của AB và AC.
Từ đó suy ra FK là đường trung bình của tam giác BAC hay \(FK=\frac{1}{2}BC\).