Cho hình vuông ABCD. Một \(\widehat{xOy}=45^0\) có Ax cắt BC tại E. Ay cắt CD tại E. Trên tia đối của tia DC lấy điểm G sao cho GD=BE
a, Tính \(\widehat{FAG}\)
b, C/m: EF=BE+DF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

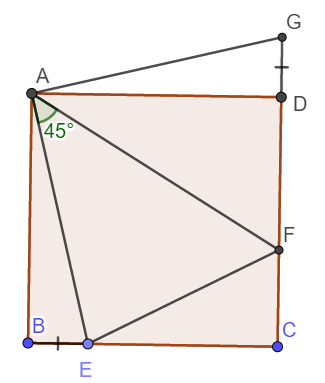
a) Xét tam giác vuông ABE và ADG có:
BE = DG (gt)
AB = AD
\(\Rightarrow\Delta ABE=\Delta ADG\) (Hai cạnh góc vuông)
\(\Rightarrow\widehat{BAE}=\widehat{DAG}\) (Hai góc tương ứng)
\(\Rightarrow\widehat{BAE}+\widehat{FAD}=\widehat{DAG}+\widehat{FAD}\)
\(\Rightarrow\widehat{BAE}+\widehat{FAD}=\widehat{FAG}\)
Mà \(\widehat{BAE}+\widehat{FAD}=90^o-\widehat{EAF}=45^o\) nên \(\widehat{FAG}=45^o\)
b) Do \(\Delta ABE=\Delta ADG\Rightarrow AE=AG\)
Xét tam giác AEF và AGF có:
AE = AG (cmt)
Cạnh AF chung
\(\widehat{EAF}=\widehat{GAF}\left(=45^o\right)\)
\(\Rightarrow\Delta AEF=\Delta AGF\left(c-g-c\right)\)
\(\Rightarrow EF=GF=FD+DG=FD+BE\)

Gọi giao điểm của IK và FE là O
ΔIOE và ΔFOK cùng vuông tại O có:
DE chung
IEOˆ=OFKˆ (vì IE // CD)
ΔIOE = ΔFOK (cgv - gnk)
=> IE = KF (tương ứng)
Có: F,KϵCDF,KϵCD mà IE // CD => KF // IE
Xét tứ giác FIEK có:
IE // KF (cmt)
IE = KF (cmt)
FIEK là hình bình hành (dhnb) có 2 đường chéo IK ⊥⊥ FE (gt) \Rightarrow FIEK là hình thoi

a: Sửa đề: ΔAEF vuông cân tại A
Xét ΔADF vuông tại D và ΔABE vuông tại B có
AD=AB
DF=BE
Do đó: ΔADF=ΔABE
=>AF=AE và \(\widehat{DAF}=\widehat{BAE}\)
mà \(\widehat{BAE}+\widehat{DAE}=90^0\)
nên \(\widehat{DAF}+\widehat{DAE}=90^0\)
=>\(\widehat{FAE}=90^0\)
Xét ΔAEF có \(\widehat{FAE}=90^0\) và AE=AF
nên ΔAEF vuông cân tại A
b: Gọi giao điểm của AH với EF là M
H đối xứng A qua EF
=>EF là đường trung trực của HA
=>EH=EA và FH=FA
mà AH=AE
nên EH=EA=FH=FA
Xét tứ giác AEHF có
AE=HE=HF=FA
nên AEHF là hình thoi
Hình thoi AEHF có \(\widehat{FAE}=90^0\)
nên AEHF là hình vuông

b: góc FAK=góc FCK=90 độ
=>ACFK nội tiếp
=>góc CAF=góc CKF
a: góc AKF=180 độ-góc ACF=180 độ-90 độ-45 độ=45 độ
=>ΔAKF vuông cân tại A

a) Xét \(\Delta\)BAE và \(\Delta\)DAC có: ^BAE = ^DAC ( đối đỉnh ) ; AD = AB ( gt ) ; AE = AC ( gt )
=> \(\Delta\)BAE = \(\Delta\)DAC ( c.g.c)
=> BE = DC
b) Tương tự câu a dễ dàng cm đc: \(\Delta\)ADE = \(\Delta\)ABC => ^ADE = ^ABC => DE//BC
=> ^EDI = ^DIC mà ^EDI = ^BDI ( DI là phân giác ^BDE )
=> ^DIC = ^BDI hay ^DIB = ^IDB => \(\Delta\)BDI cân tại B.
c) Ta có: ^DBC là góc ngoài tại đỉnh B của \(\Delta\)BDI => ^DBC = ^BDI + ^BID = 2. ^BID = 2. ^CIF( theo b) (1)
Có: CF là phân giác ^BCA =>^BCF = ^ACF => ^BCA = ^BCF + ^ACF = 2. ^BCF = 2. ^ICF (2)
Lại có: ^CFD là góc ngoài của \(\Delta\)FCI => ^CFD = ^CIF + ^ICF (3)
Từ (1) ; (2) ; (3) => 2 .^CFD = 2 ^CIF + 2. ^ICF = ^DBC + ^BCA = ^DBC + ^CED ( ^CED = ^BCA vì ED //BC )
\(\widehat{xAy}=45^0nha\)
sao trên đề ghi có hai đoạn cắt tại E vậy bn