Gọi M là điểm nằm trong góc xOy = mo(o<m<90). Gọi P,Q lần lượt là hình chiếu của M trên Ox,Oy. Gọi H,K lần lượt là trung điểm của OM,PQ
a) Chứng minh HK⊥PQ
b) Tính số đo góc HPQ theo m
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét $(O)$ có: $\widehat{MCA}=\widehat{CBA}$ (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung $CA$)
hay $\widehat{MCA}=\widehat{MBC}$
Xét $ΔMCA$ và $ΔMBC$ có:
$\widehat{MCA}=\widehat{MBC}$
$\widehat{M}$ chung
$⇒ΔMCA \backsim ΔMBC(g.g)$
\(\Rightarrow\dfrac{MC}{MB}=\dfrac{MA}{MC}\Rightarrow MC^2=MA.MB\)
b, Xét $(O)$ có: $MC$ là tiếp tuyến của đường tròn
\(\Rightarrow MC\perp OC\)
hay $ΔMCO$ vuông tại $C$
có: đường cao $MH$
nên $MC^2=MH.MO$ (hệ thức lượng trong tam giác vuông)
Mà $MC^2=MA.MB$ nên $MA.MB=MH.MO$
suy ra \(\Rightarrow\dfrac{MA}{MO}=\dfrac{MH}{MB}\)
$\widehat{M}$ chung
Nên $ΔMAH \backsim ΔMOB(c.g.c)$
nên $\widehat{MHA}=\widehat{MBO}$
hay $\widehat{MHA}=\widehat{ABO}$
suy ra tứ giác $AHOB$ nội tiếp (góc ngoài tại 1 đỉnh = góc trong đỉnh đối diện)

Gọi giao điểm của MN và Ox là điểm A; giao điểm của MN và Oy là điểm B.
Ta có: N là điểm đối xứng với M qua Ox (gt).
O \(\in\) Ox.
=> \(\left\{{}\begin{matrix}OA\perp MN.\\\text{ON = OM.(1)}\end{matrix}\right.\)
Ta có: P là điểm đối xứng với M qua Oy (gt).
O \(\in\) Oy.
=> \(\left\{{}\begin{matrix}OB\perp MP.\\\text{OM = OP.(2)}\end{matrix}\right.\)
Từ (1) và (2) => OP = ON = OM.
Xét tam giác NOM có: ON = OM (cmt).
=> Tam giác NOM cân tại O.
Mà OA là đường cao (do OA vuông góc MN).
=> OA là phân giác của ^NOM (Tính chất các đường trong tam giác cân).
=> ^NOA = ^AOM.
Xét tam giác MOP có: OP = OM (cmt).
=> Tam giác MOM cân tại O.
Mà OB là đường cao (do OB vuông góc MP).
=> OB là phân giác của ^MOP (Tính chất các đường trong tam giác cân).
=> ^MOB = ^BOP.
Ta có: ^NOA + ^AOM + ^MOB + ^BOP.
= 2. ^AOM + 2. ^MOB.
= 2. (^AOM + ^MOB).
= 2. ^AOB.
= 2. 90o = 180o.
=> 3 điểm N; O; P thẳng hàng.
Mà OP = ON (cmt).
=> O là trung điểm của NP.
=> P và N đối xứng nhau qua O (đpcm).

Theo đề bài ta có I là trung điểm đoạn EF => I thuộc tia phân giác góc xOy => góc EOI = góc FOI
Cho H,K là chân các đường vuông góc hạ từ M xuống các tia Ox, Oy => \(MH⊥Ox;MK⊥Oy\)(1)
ta có : góc MHO = góc MKO = 900
=> tứ giác OHMK nội tiếp => góc MOK = góc MHK(cùng chắn cung MK),góc MOH = góc HKM (cùng chắn cung HM)
Mà góc MOK = góc MOH (cmt) nên góc MHK = góc HKM => tam giác MHK cân tại M => MH = MK (2)
Từ (1) và (2) => M thuộc đường phân giác của góc xOy
Vì I và M đều thuộc tia phân giác của góc xOy nên I,OM thẳng hàng
p/s còn nhiều cách khác .vd: (dùng hình vẽ trên) : chứng minh 2 tam giác HMO = tam giác KMO( tam giác vuông có cạnh OM chung và góc HOM = góc MOK) => MH=MK -> phần sau làm tương tự.............[cách này ngắn hơn nhưng không dùng cho lớp 9 HKII]

a: OH*OM=OA^2=R^2
b: ΔOCD cân tại O
mà OI là đường trung tuyến
nên OI vuông góc với CD
Xét tứ giác OIAM có
góc OIM=góc OAM=90 độ
nên OIAM là tứ giác nội tiếp
c: Xét ΔOHK vuông tại H và ΔOIM vuông tại I có
góc HOK chung
Do đo: ΔOHK đồng dạng với ΔOIM
=>OH/OI=OK/OM
=>OI*OK=OH*OM=R^2=OC^2
mà CI vuông góc với OK
nên ΔOCK vuông tại C
=>KC là tiếp tuyến của (O)

a: Xét tứ giác MAOB có
góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
b: Xét ΔMAN và ΔMPA có
góc MAN=góc MPA
góc AMN chung
=>ΔMAN đồng dạng với ΔMPA
=>MA/MP=MN/MA
=>MA^2=MN*MP
c: Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM vuông góc AB tại i
Xét ΔOAM vuông tại A có AI là đường cao
nên OI*OM=OA^2
=>OI*OM=R^2 ko đổi

`a)`
Có `IH⊥Ox=>hat(H_1)=90^0`
`IK⊥Oy=>hat(K_1)=90^0`
Xét `Delta KIO` và `Delta HIO` có :
`{:(hat(K_1)=hat(H_1)(=90^0)),(OI-chung),(IK=IH(GT)):}}`
`=>Delta KIO=Delta HIO(c.h-c.g.v)(đpcm)`
`b)`
Có `Delta KIO=Delta HIO(cmt)=>hat(O_1)=hat(O_2)` ( 2 góc t/ứng )
mà `OI` nằm giữa `Ox` và `Oy(I in hat(xOy))`
nên `OI` là p/g của `hat(xOy)(đpcm)`

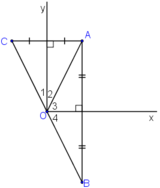
+ B đối xứng với A qua Ox
⇒ Ox là đường trung trực của AB
⇒ OA = OB (1)
+ C đối xứng với A qua Oy
⇒ Oy là đường trung trực của AC
⇒ OA = OC (2)
Từ (1) và (2) suy ra OB = OC (*).
+ Xét ΔOAC cân tại O (do OA = OC) có Oy là đường trung trực
⇒ Oy đồng thời là đường phân giác
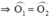
Xét ΔOAB cân tại O có Ox là đường trung trực
⇒ Ox đồng thời là đường phân giác
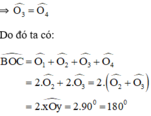
⇒ B, O, C thẳng hàng (**)
Từ (*) và (**) suy ra O là trung điểm BC
⇒ B đối xứng với C qua O.