Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét (O) có
ΔNEI nội tiếp đường tròn
NI là đường kính
Do đó: ΔNEI vuông tại E
hay NE⊥MI
Xét (O) có
ΔNDI nội tiếp đường tròn
NI là đường kính
Do đó: ΔNDI vuông tại D
hay ID⊥MN
b: Xét ΔMNI có
ID là đường cao ứng với cạnh MN
NE là đường cao ứng với cạnh MI
NE cắt ID tại H
Do đó: MH⊥NI
a: Xét (O) có
ΔNEI nội tiếp đường tròn
NI là đường kính
Do đó: ΔNEI vuông tại E
Xét (O) có
ΔNDI nội tiếp đường tròn
NI là đường kính
Do đó: ΔNDI vuông tại D
\(a,\)Gọi tâm đường tròn đường kính NI là O
Ta có \(OE=OD=ON=OI\left(=R\right)=\dfrac{1}{2}IN\)
\(\Rightarrow\Delta INE,\Delta IND\) lần lượt vuông tại \(E,D\)
\(\Rightarrow NE\perp MI,ID\perp MN\)
\(b,\) Tam giác MNI có NE, ID là đường cao; H là giao điểm NE và ID nên H là trực tâm
\(\Rightarrow MH\) là đường cao thứ 3
\(\Rightarrow MH\perp NI\)
Câu 1:
a: Xét (\(\dfrac{NI}{2}\)) có
ΔNEI nội tiếp đường tròn
NI là đường kính
Do đó: ΔNEI vuông tại E
Xét \(\left(\dfrac{NI}{2}\right)\) có
ΔNDI nội tiếp đường tròn
NI là đường kính
Do đó: ΔNDI vuông tại D
b: Xét ΔMNI có
NE là đường cao ứng với cạnh MI
ID là đường cao ứng với cạnh MN
NE cắt ID tại H
Do đó: MH\(\perp\)NI
Đề bài sai nhiều quá, em kiểm tra lại câu a là ON hay MN, và câu b là ON hay MN?
a) Xét tam giác PNK vuông tại P và tam giác INK vuông tại I có:
\(\widehat{N}=\widehat{K}\)(tam giác MNK là tam giác cân)
NK:chung
Suy ra \(\Delta PNK=\Delta INK\)(cạnh huyền-góc nhọn)
=>PN=IK(1)
Mà do MNK cân tại M nên MN=MK(2)
Từ (1) và (2), suy ra MI=MP
b)Từ a) ta suy ra: \(\widehat{HNK}=\widehat{HKN}\)(hai góc tương ứng)<=> \(\widehat{IKH}=\widehat{PNH}\)
Xét tam giác PHN vuông tại P và tam giác IHK vuông tại I có:
\(NP=IK\left(cmt\right)\)
\(\widehat{IKH}=\widehat{PNH}\)(cmt)
Suy ra:....(cạnh góc vuông-góc nhọn kề)
=>HP=HI
Xét tam giác PMH và tam giác HMI có:
MH:chung
MP=MI(cmt)
HP=HI(cmt)
Suy ra:....(c-c-c)
=> \(\widehat{PMH}=\widehat{IMH}\)(hai góc tương ứng )
=>MH là tia phân giác của góc M
c) Từ b) suy ra MP=MI(2 cạnh tương ứng)
=>PMI là tam giác cân
Xét tam giác PMI có:
\(\widehat{P}=\widehat{I}=\frac{180^o-\widehat{M}}{2}\left(1\right)\)
Xét tam giác MNK có:
\(\widehat{K}=\widehat{N}=\frac{180^o-\widehat{M}}{2}\left(2\right)\)
=>\(\widehat{K}=\widehat{N}=\widehat{P}=\widehat{I}\)
Mà các cặp góc này ở vị trí đồng vị nên PI//NK
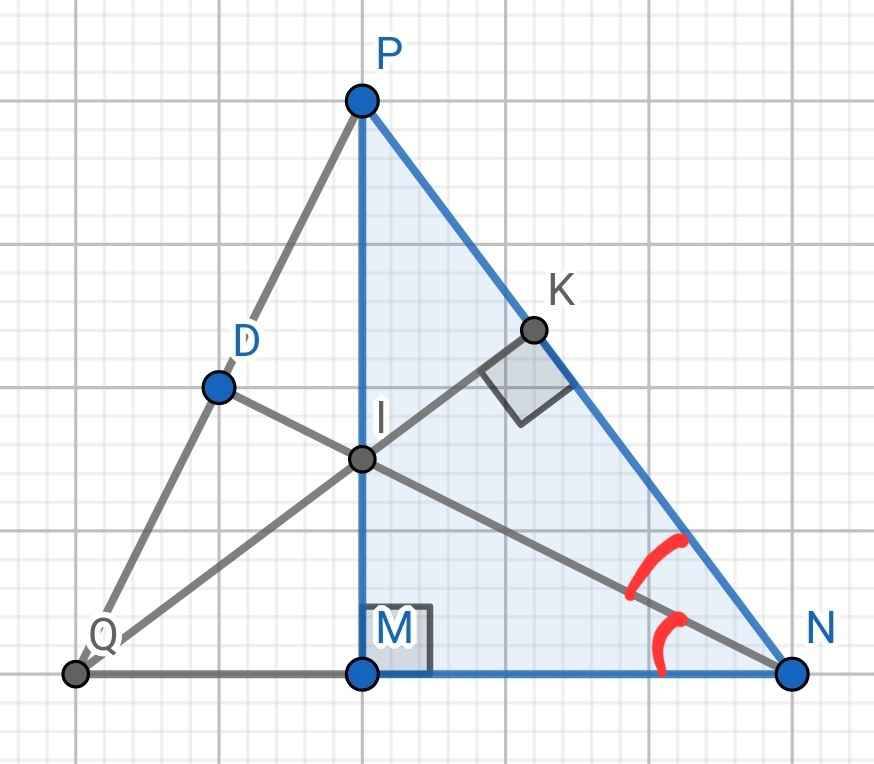
a) Xét hai tam giác vuông: ∆IMN và ∆IKN có:
IN chung
MNI = KNI (do NI là phân giác của ∠MNP)
⇒ ∆IMN = ∆IKN (cạnh huyền - góc nhọn)
b) ∆IKP vuông tại K
IP là cạnh huyền nên IP lớn nhất
IK < IP (1)
Do ∆IMN = ∆IKN (cmt)
⇒ MI = IK (2)
Từ (1) và (2)⇒ MI < IP
c) Xét hai tam giác vuông: ∆IKP và ∆IMQ có:
IM = IK (cmt)
∠PIK = ∠MIQ (đối đỉnh)
∆IKP = ∆IMQ (cạnh góc vuông - góc nhọn kề)
⇒ KP = MQ (hai cạnh tương ứng) (3)
Do ∆IMN = ∆IKN (cmt)
⇒ MN = KN (hai cạnh tương ứng) (4)
Từ (3) và (4) ⇒ KN + KP = MN + MQ
NP = NQ
⇒ ∆NPQ cân tại N
Lại có NI là phân giác của ∠MNP
⇒ NI là phân giác của ∠QNP
⇒ NI cũng là đường cao của ∆NPQ (tính chất tam giác cân)
⇒ ND ⊥ QP
a: Xét (O) có
ΔNEI nội tiếp đường tròn
NI là đường kính
Do đó: ΔNEI vuông tại E
Xét (O) có
ΔNDI nội tiếp đường tròn
NI là đường kính
Do đó: ΔNDI vuông tại D
HT , đúng thì k nhé