Cho đa thức f (x) = ax2 + bx + c ( a,b,c \(\in\) Z ) Biết f (-1) ; f (0) ; f (1) đều chia hết cho 3 . CM : a\(⋮\) 3; b \(⋮\) 3; c\(⋮\) 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 4 2018
Ta có : a + c = b + 2018
b = a + c - 2018
f(-1) = a . ( -1 )2 + b . ( -1 ) + c = a - b + c = a - ( a + c - 2018 ) + c = a - a - c + 2018 + c = 2018
AH
Akai Haruma
Giáo viên
13 tháng 5 2021
Lời giải:
$f(1)=a+b+c=6$
$f(2)=4a+2b+c=16$
$f(12)-f(-9)=(144a+12b+c)-(81a-9b+c)$
$=63a+21b=21(3a+b)$
$=21[(4a+2b+c)-(a+b+c)]=21(16-6)=21.10=210$
MC
7 tháng 5 2018
Theo đề ta có : a + c = b + 2018
=> a + c -b = 2018
Ta có f(-1) = a.(-1)2 + b.(-1) + c = a - b + c = 2018
CM
11 tháng 1 2018
Chọn A.
Theo giả thiết, ta có:
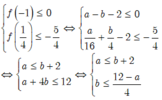
Khi đó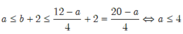 
Vậy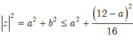 
Xét hàm số 
với 
, có 
Tính các giá trị 
suy ra 
Vậy giá trị lớn nhất của
z
là: 
HP
1
8 tháng 5 2018
Bạn ơi bạn thử kiểm tra kỹ xem cái đề bài hộ mình cái bởi vì mình thay x = 1 x = -1 vào đa thức nhưng không bằng nhau.
Sửa là ax2-bx+c
Mk đoán thôi
KH
11 tháng 5 2021
\(a.f\left(1\right)=f\left(-1\right)\Leftrightarrow a+b+c=a-b+c\Leftrightarrow2b=0\Leftrightarrow b=0\)
\(\Rightarrow f\left(x\right)=ax^2+c\)
Khi đó ta có:
\(\left\{{}\begin{matrix}f\left(m\right)=am^2+c\\f\left(-m\right)=am^2+c\end{matrix}\right.\Rightarrow f\left(m\right)=f\left(-m\right)\forall m\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 3 2021
\(f\left(0\right)=c⋮3\) ;
\(f\left(1\right)=a+b+c⋮3\) mà \(c⋮3\Rightarrow a+b⋮3\)
\(f\left(-1\right)=a-b+c=-2b+\left(a+b+c\right)⋮3\) mà \(a+b+c⋮3\Rightarrow-2b⋮3\Rightarrow b⋮3\) (do 2 và 3 nguyên tố cùng nhau)
\(\left\{{}\begin{matrix}a+b+c⋮3\\b⋮3\\c⋮3\end{matrix}\right.\) \(\Rightarrow a⋮3\)
9 tháng 5 2023
a: f(1)=a+b+c=0
=>x=1 là nghiệm
b: Vì 5-6+1=0
nên f(x)=5x^2-6x+1 có một nghiệm là x=1
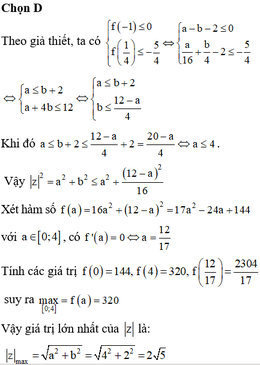
Ta có: f(0) = c \(⋮\) 3
f(1) = a + b + c \(⋮\) 3 \(\Rightarrow\) a + b \(⋮\) 3 (1)
f(-1) = a - b + c \(⋮\) 3 \(\Rightarrow\) a - b \(⋮\) 3 (2)
Từ (1) và (2) suy ra a + b + a - b \(⋮\) 3 và a + b - a + b \(⋮\) 3
\(\Rightarrow\) \(\left\{{}\begin{matrix}2a⋮3\\2b⋮3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a⋮3\\b⋮3\end{matrix}\right.\)
Vậy a, b, c \(⋮\) 3
+ \(\left\{{}\begin{matrix}f\left(0\right)⋮3\\f\left(1\right)⋮3\\f\left(-1\right)⋮3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}c⋮3\\a+b+c⋮3\\a-b+c⋮3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a+b⋮3\\a-b⋮3\\c⋮3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2a⋮3\\-2b⋮3\\c⋮3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a⋮3\\b⋮3\\c⋮3\end{matrix}\right.\)