Cho đường tròn tâm (O; R) và một điểm A cố định trên đường tròn đó. Qua A vẽ
tiếp tuyến xy. Từ một điểm M trên xy vẽ tiếp tuyến MB với đường tròn (O). Hai đường cao AD
và BE của tam giác MAB cắt nhau tại H; MO cắt AB tại K.
1. Chứng minh OM là trung trực của AB.
2. Chứng minh rằng tứ giác AOBH là hình thoi.
3. Chứng minh OK. OM có giá trị không đổi.
4. Khi điểm M di động trên xy thì điểm H di động trên đường nào?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

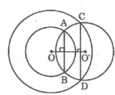
Vì đường tròn (O’) cắt đường tròn (O ; OA) tại A và B nên OO’ là trung trực của AB
Suy ra : OO’ ⊥ AB (1)
Vì đường tròn (O’) cắt đường tròn (O ; OC) tại C và D nên OO’ là trung trực của CD
Suy ra : OO’ ⊥ CD (2)
Từ (1) và (2) suy ra : AB // CD.

a: ΔOAB cân tại O
mà OM là đường cao
nên OM là phân giác
Xét ΔOAM và ΔOBM có
OA=OB
góc AOM=góc BOM
OM chung
=>ΔOAM=ΔOBM
=>góc OBM=90 độ
=>MB là tiếp tuyến của (O)
b:F ở đâu vậy bạn?

Đáp số:a)12,56cm
b)bằng nhau các bạn nhớ k cho mình nha mình đang bị âm điểm ^_^
A B O M N
a, Chu vi của hình tròn tâm O là:
8 x 3,14 = 25,12 (cm)
Đường kính AO có độ dài là:
8 : 2 = 4 (cm)
Chu vi của hình tròn tâm M là:
4 x 3,14 = 12,56 (cm)
Đường kính OB có độ dài là:
8 - 4 = 4 (cm)
Chu vi của hình tròn tâm N là:
4 x 3,14 = 12,56 (cm)
b, Tổng chu vi của hai hình tròn tâm M và N là:
12,56 + 12,56 = 25,12 (cm)
Vì 25,12 = 25,12 (cm) nên tổng chu vi của hai hình tròn tâm M và N = chu vi hình tròn tâm O.
Đáp số: a, 25,12 cm; 12,56 cm; 12,56 cm
b, bằng nhau