Cho hình thang ABCD có : AB = 4cm , CD = 16cm và BD = 8cm . a) Chứng minh : góc BAD = góc DBC . b) Gọi AD giao với BD tại M và BC = 6cm . Tính MC . c) Vẽ AH vuông BD tại H , DK vuông CD tại K . Chứng minh : S tam giác BKC = 4S tam giác ADH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔAHD vuông tại H và ΔBAD vuông tại A có
góc D chung
=>ΔAHD đồng dạng với ΔBAD
b; Xét ΔDEA vuông tại D và ΔADB vuông tại A có
góc DEA=góc ADB
=>ΔDEA đồng dạng với ΔADB
=>DE/AD=AD/AB
=>AD^2=DE*AB
c: AD^2=DE*AB
=>DE=3^2/4=2,25cm

a: Xét ΔFAB và ΔFCD có
góc FAB=góc FCD
góc AFB=góc CFD
=>ΔFAB đồng dạng với ΔFCD
b: ΔFAB đồng dạng với ΔFCD
=>FA/FC=FB/FD
=>FA*FD=FB*FC

a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
Suy ra:AN//CM

Ta có: 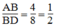
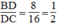
Suy ra: 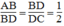
Xét △ ABD và △ BDC, ta có:
∠ (ABD) = ∠ (BDC) (so le trong)
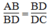 (chứng minh trên)
(chứng minh trên)
Vây △ ABD đồng dạng △ BDC (c.g.c) ⇒ ∠ (BAD) = ∠ (DBC)
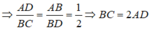
Tỉ số đồng dạng k = 1/2
Ta có: 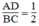 , suy ra: BC = 2AD
, suy ra: BC = 2AD
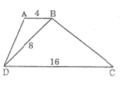
a: Xét ΔABD và ΔBDC có
AB/BD=BD/DC
\(\widehat{ABD}=\widehat{BDC}\)
Do đo: ΔABD\(\sim\)ΔBDC
b: Sửa đề: AD cắt BC tại M
Xét ΔMDC có AB//DC
nên AB/DC=MB/MC
=>MB/MC=4/16=1/4
\(\Leftrightarrow MC=4MB\)
\(\Leftrightarrow4MB=MB+6\)
=>MB=2
=>MC=6+2=8cm