Cho tam giác đều và một lục giác đều có chu vi bằng nhau. Nếu diện tích tam giác bằng \(4\sqrt{3}\) cm2 thì diện tích lục giác là bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

M
24 tháng 8 2023
Đúng, tam giác đều có 3 cạnh bằng nhau và ba góc bằng nhau.Đúng, tam giác đều có cạnh là a thì chu vi là 3a.Đúng, lục giác đều có cạnh là a thì chu vi là 6a.Sai, trong lục giác đều các đường chéo không bằng nhau.Sai, hình vuông có cạnh là 5m thì diện tích là 25m2.Đúng, trong lục giác đều ABCDEG, các đường chéo chính AD, BE, CG cắt nhau tại điểm O thì OA = OB = OC = OD = OE = OG.

5 tháng 1 2023
Nếu chiều cao và đáy tương ứng tăng gấp đôi thì diện tích thì diện tích hình tam giác tăng:
2 x 2 = 4 (lần)
Diện tích hình tam giác lúc đó là:
25 x 4 = 100 (cm2)
Đáp số: 100 cm2
AH
Akai Haruma
Giáo viên
5 tháng 1 2023
Lời giải:
Khi độ dài đáy và chiều cao cùng tăng gấp đôi thì diện tích tăng $2\times 2=4$ (lần)
Diện tích tam giác lúc đó là: $25\times 4=100$ (cm2)
Gọi tam giác đều đã cho là tam giác ABC.
Kẻ đường cao AH . Tam giác ABC đều nên AH là đường trung tuyến => H là trung điểm của BC => BH = BC/2 = AB/2
Áp dụng ĐL Pi ta go trong tam giác vuông ABH có: AH2 = AB2 - BH2 = AB2 - AB2/4 = 3AB2/4 => AH = \(\frac{AB\sqrt{3}}{2}\)
S(ABC) = AH.BC/2 = \(\frac{AB^2\sqrt{3}}{4}=4\sqrt{3}\) => AB2 = 16 => AB = 4 cm
=> Chu vi tam giác đều ABC là: AB .3 = 12 cm
+) Tổng quát : Kí hiệu a là cạnh của tam giác đều => S tam giác đều = \(\frac{a^2\sqrt{3}}{4}\) (*)
+) Chu vi lục giác đều bằng 12 cm => cạnh của lục giác đều là: 12 : 6 = 2 cm
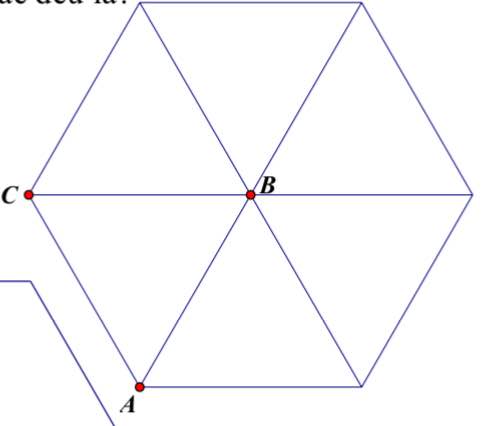
Chia lục giác đều thành 6 tam giác đều bằng nhau có cạnh bằng cạnh của lục giác đó
Áp dụng công thức (*) => Diện tích 1 tam giác = \(\frac{4\sqrt{3}}{4}=\sqrt{3}\) cm2
Diện tích lục giác = 6 x Diện tích 1 tam giác = \(6\sqrt{3}\) cm2
ĐS:...