Cho tam giác ABC có AB = 3, AC = 4, BC = 5.
a) Xác định tâm O và bán kính của đường tròn ngoại tiếp tam giác ABC.
b) Gọi D là điểm đối xứng của A qua BC. Chứng minh D thuộc (O) và tính diện tích tam giác BCD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 9 2021
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Suy ra: ΔABC nội tiếp đường tròn đường kính BC
hay O là trung điểm của BC
\(R=\dfrac{BC}{2}\)
CM
23 tháng 4 2018
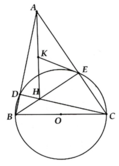
a, HS tự chứng minh
b, HS tự chứng minh
c, DAEH vuông nên ta có: KE = KA = 1 2 AH
=> DAKE cân tại K
=> K A E ^ = K E A ^
DEOC cân ở O => O C E ^ = O E C ^
H là trực tâm => AH ^ BC
Có A E K ^ + O E C ^ = H A C ^ + A C O ^ = 90 0
(K tâm ngoại tiếp) => OE ^ KE
d, HS tự làm
15 tháng 4 2020
Cho △ABC nhọn (AB<AC) nội tiếp (O), 2 đường cao BD và CE cắt nhau tại H
a/ Chứng minh : B,C,D,E cùng nằm trên một đường tròn .Xác định tâm M của đường tròn này.
b/ Chứng minh : OM // AH
c/ Chứng minh : AB.AE = AC.AD
d/ Gọi K là điểm đối xứng của H qua M .
CM
27 tháng 3 2018
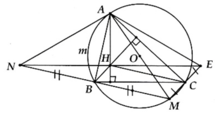
a, BH ^ AC và CM ^ AC Þ BH//CM
Tương tự => CH//BM
=> BHCM là hình bình hành
b, Chứng minh BNHC là hình bình hành
=> NH//BC
=> AH ^ NH => A H M ^ = 90 0
Mà A B N ^ = 90 0 => Tứ giác AHBN nội tiếp
c, Tương tự ý b, ta có: BHEC là hình bình hành. Vậy NH và HE//BC => N, H, E thẳng hàng
d, A B N ^ = 90 0 => AN là đường kính đường tròn ngoại tiếp tứ giác AHBN
AN = AM = 2R, AB = R 3 => A m B ⏜ = 120 0
S A O B = 1 2 S A B M = R 2 3 4
S A m B ⏜ = S a t A O B - S A O B = R 2 12 4 π - 3 3
=> S cần tìm = 2 S A m B ⏜ = R 2 6 4 π - 3 3
CM
5 tháng 10 2019
a, Học sinh tự chứng minh
b, Học sinh tự chứng minh
c, Học sinh tự chứng minh
d, Chú ý: B I A ^ = B M A ^ , B M C ^ = B K C ^
=> Tứ giác BICK nội tiếp đường tròn (T), mà (T) cũng là đường tròn ngoại tiếp DBIK. Trong (T), dây BC không đổi mà đường kính của (T) ≥ BC nên đường kính nhỏ nhất bằng BC
Dấu "=" xảy ra <=> B I C ^ = 90 0 => I ≡ A => MA
11 tháng 9 2021
https://mathx.vn/uploads/ho-tro-hoc-tap/vip/images/Screenshot_38.png
CL
12 tháng 9 2021
a) Vẽ đường trung trực A H của cạnh B C . Qua trung điểm I của cạnh A B vẽ trung trực cạnh A B cắt A H tại O chính là tâm đường tròn ngoại tiếp của tam giác A B C Theo định lý pi ta go: A H 2 = A B 2 − B H 2 = 5 2 − 3 2 = 16 => A H = 4 Tam giác vuông A O I đồng dạng tam giác vuông A B H (chung góc A ) nên: A O A I = A B A H => R = A O = A B . A I A H = 5.2 , 5 4 = 3 , 125 b) Vì B D là đk nên tam giác A B D vuông A B D = 2 R = 6 , 26 . Theo Py ta go: A D 2 = B D 2 − A B 2 = 6 , 25 2 − 5 2 = 14 , 0625 => A D = 3 , 75 Tương tự tam giác C B D vuông C C D 2 = B D 2 − B C 2 = 6 , 25 2 − 6 2 = 3 , 0625 => C D = 1 , 75
a: Xét ΔABC có
\(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Suy ra: ΔABC nội tiếp đường tròn đường kính BC
hay O là trung điểm của BC
\(\Leftrightarrow R=\dfrac{BC}{2}\)