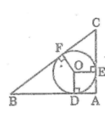
Cho tam giác ABC ( AB < AC ) nội tiếp đường tròn ( O ; R ) có 2 đường cao BD, CE cắt nhau tại H, AH cắt BC tại F.
a) C/m ADHE nội tiếp rồi xác định tâm
b) Vẽ tia Cx là tiếp tuyến của (O; R) ( tia Cx nằm trên 1 nửa mặt phẳng bờ là BC không chứa điểm A ). C/m Cx // DF

Lời giải:
a) Vì $BD, CE$ là đường cao nên \(BD\perp AC, CE\perp AB\)
\(\Rightarrow \widehat{HDA}=\widehat{HEA}=90^0\)
\(\Rightarrow \widehat{HDA}+\widehat{HEA}=180^0\)
Do đó tứ giác $ADHE$ nội tiếp.
Gọi $I$ là trung điểm của $AH$ thì \(AI=IH=\frac{AH}{2}\)
Xét tam giác $AEH$ vuông tại $E$ có $I$ là trung điểm cạnh huyền $AH$ nên \(EI=\frac{AH}{2}\) (theo định lý về đường trung tuyến đối diện cạnh huyền của tam giác vuông).
Hoàn toàn tương tự \(DI=\frac{AH}{2}\)
Do đó: \(AI=HI=EI=DI\Rightarrow I\) là tâm đường tròn ngoại tiếp tứ giác $ADHE$
b)
Vì ba đường cao của tam giác thì đồng quy tại một điểm nên hiển nhiên $AF$ là đường cao của tam giác $ABC$
\(\Rightarrow \widehat{ADB}=\widehat{AFB}=90^0\)
\(\Rightarrow ADFB\) nội tiếp.
\(\Rightarrow \widehat{DAB}+\widehat{DFB}=180^0\) (hai góc đối nhau)
Mà \(\widehat{DFB}+\widehat{DFC}=180^0\Rightarrow \widehat{DAB}=\widehat{DFC}(1)\)
Lại có: \(\widehat{DAB}=\widehat{BCx}\) (cùng chắn cung BC)
Do đó: \(\widehat{DFC}=\widehat{BCx}\), mà hai góc này ở vị trí so le trong nên \(Cx\parallel DF\)
Ta có đpcm.