giúp em bài 9,10 với ạ,em c ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(CT:C_xH_yO_z\)
\(x:y:z=\dfrac{54.54}{12}:\dfrac{9.1}{1}:\dfrac{36.36}{16}=4.545:9.1:2.2725=2:4:1\)
\(CTnguyên:\left(C_2H_4O\right)_n\)
\(M_X=88\)
\(\Leftrightarrow44n=88\)
\(\Leftrightarrow n=2\)
\(CTPT:C_4H_8O_2\)
Chúc bạn học tốt !!


Bài 3:
\(a,=3x\left(y-4x+6y^2\right)\\ b,=5xy\left(x^2-6x+9\right)=5xy\left(x-3\right)^2\\ d,=\left(x+y\right)\left(x-12\right)\\ f,=2x\left(x-y\right)\left(5x-4y\right)\\ g,=\left(x-2\right)\left(x-2+3x\right)=\left(x-2\right)\left(4x-2\right)=2\left(x-2\right)\left(2x-1\right)\\ h,=x^2\left(1-5x\right)+3xy\left(5x-1\right)=x\left(1-5x\right)\left(x-3y\right)\\ i,=x\left(x-2\right)+4\left(x-2\right)=\left(x+4\right)\left(x-2\right)\\ j,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ k,=4x^2-12x+3x-9=\left(x-3\right)\left(4x+3\right)\\ l,=\left(x+5\right)^2-y^2=\left(x-y+5\right)\left(x+y+5\right)\\ m,=x^2-\left(2y-6\right)^2=\left(x-2y+6\right)\left(x+2y-6\right)\\ n,=\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24\\ =\left(x^2+5x+5\right)^2-1-24\\ =\left(x^2+5x+5\right)^2-25\\ =\left(x^2+5x\right)\left(x^2+5x+10\right)\\ =x\left(x+5\right)\left(x^2+5x+10\right)\)

Bài 1:
a: =3x(x+2)
b: \(=x\left(x-1\right)^2\)
c: \(=x^2\left(x-y\right)-\left(x-y\right)=\left(x-y\right)\left(x-1\right)\left(x+1\right)\)

a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM⊥AB

a) \(BC^2=AB^2+AC^2\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)
\(\left\{{}\begin{matrix}sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\Rightarrow\widehat{B}\approx53^0\\sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\Rightarrow\widehat{C}=37^0\end{matrix}\right.\)
c) Ta có: \(\left\{{}\begin{matrix}AB=BD\\AC=DC\end{matrix}\right.\)(t/c 2 tiếp tuyến cắt nhau)
=> BC là đường trung trực AD
\(\Rightarrow AD\perp BC\)
Áp dụng HTL trong tam giác BDC vuông tại D:
\(FB.FC=FD^2\Rightarrow4FB.FC=4FD^2=\left(2FD\right)^2=AD^2\)

Bài 13:
góc A=180-80-30=70 độ
=>góc BAD=góc CAD=70/2=35 độ
góc ADC=80+35=115 độ
góc ADB=180-115=65 độ
Bài 14:
Xét ΔABC vuông tại A
-> \(\widehat{B}\)\(+ \widehat{C}=90^o\)
Mà \(\widehat{B}=\widehat{C}\)
=> \(2\widehat{B}=90^o\)
=> \(\widehat{B}=45^o\)


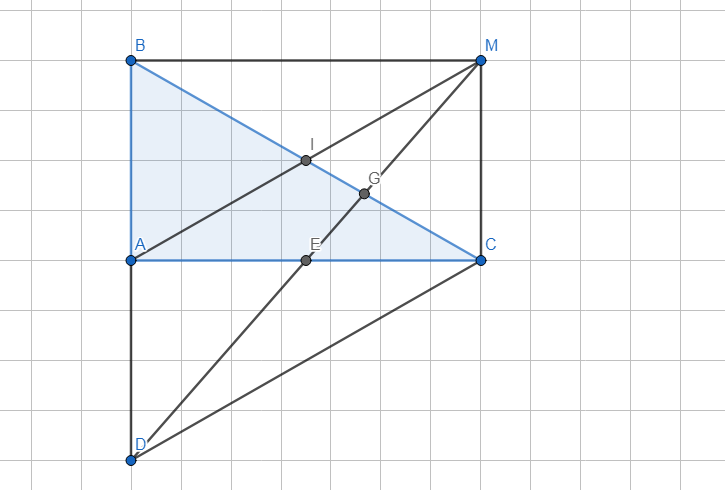

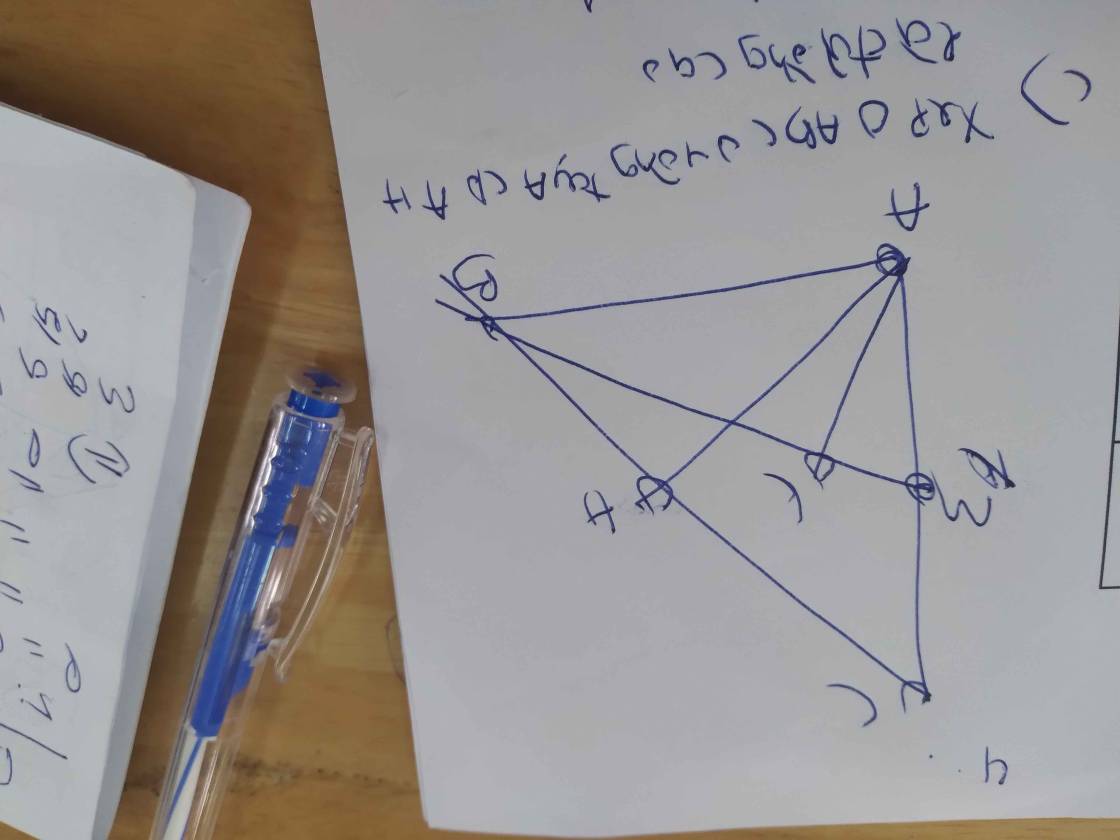





Bài 10:
a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền AB
nên \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
hay AH=2,4(cm)
Bài 9:
a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
\(\widehat{A}\) chung
Do đó: ΔABE\(\sim\)ΔACF
Suy ra: \(\dfrac{AB}{AC}=\dfrac{AE}{AF}\)
hay \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
\(\widehat{A}\) chung
Do đó: ΔAEF\(\sim\)ΔABC
b: Ta có: \(\dfrac{AE}{AB}=\dfrac{EF}{BC}\)
nên \(BC=EF:\dfrac{1}{2}=5:\dfrac{1}{2}=10\left(cm\right)\)