Tính 1-2-3+4+5-6-7+8+...+1989-1990-1991+1992+1993
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



b) 1-2-3+4+5-6-7+8+......+1989-1990-1991+1992+1993
=(1-2-3+4)+(5-6-7+8)+.....+(1989-1990-1991+1992)+1993
=0+0+...+0+1993=1993.

1991*1993-1/1990+1991*1992
=1991*(1992+1)-1/1990+1991*1992
=1991*1992+1991*1-1/1990+1991*1992
=1990/1990
=1
1991*(1993-1)-1/1990+1991*1992
= 1991*1992-1/1990+1991*1992
= 1990/1990
= 1

Bài 1
a; \(\dfrac{7}{19}\) x \(\dfrac{1}{3}\) + \(\dfrac{7}{19}\) x \(\dfrac{2}{3}\)
= \(\dfrac{7}{19}\) x (\(\dfrac{1}{3}+\dfrac{2}{3}\))
= \(\dfrac{7}{19}\) x 1
= \(\dfrac{7}{19}\)
b; 15 x \(\dfrac{2121}{4343}\) + 15 x \(\dfrac{212121}{434343}\)
= 15 x \(\dfrac{21}{43}\) + 15 x \(\dfrac{21}{43}\)
= 15 x \(\dfrac{21}{43}\) x (1 + 1)
= 15 x \(\dfrac{21}{43}\) x 2
= (15 x 2) x \(\dfrac{21}{43}\)
= 30 x \(\dfrac{21}{43}\)
= \(\dfrac{630}{43}\)

(1989.1990+3978):(1992.1991−3984)
=[1989.(1990+2)]:[1992(1991−2)]=(1989.1992):(1992.1989)=1=[1989.(1990+2)]:[1992(1991−2)]=(1989.1992):(1992.1989)=1

\(\left(1989.1990+3978\right):\left(1992.1991-3984\right)\)
\(=\left[1989.\left(1990+2\right)\right]:\left[1992\left(1991-2\right)\right]=\left(1989.1992\right):\left(1992.1989\right)=1\)

= \(\frac{1991.1992.1993.1994.995}{1990.1991.1992.1993.997}\)
= \(\frac{1994.995}{1990.997}\)
= \(\frac{997.2.995}{995.2.997}\)
= \(1\)
= \(\frac{1991.1992.1993.1994.995}{1990.1991.1992.1993.997}\)
= \(\frac{1994.995}{1990.997}\)
= \(\frac{997.2.995}{995.2.997}\)
Vì có 1 số 995 ở tử số và 1 số 995 ở mẫu số
Và có 1 số 997 ở tử số và 1 số 997 ở mẫu số
Nên hai số chỉ khác nhau điểm xoay đuôi lên đầu và xoay đầu xuống đuôi nhưng số 2 không thay đổi . Vậy Phân số tử số và mẫu số bằng nhau
Mà phân số có tử số và mẫu số bằng nhau thì phân số đó bằng 1
= 1
Đáp số : 1
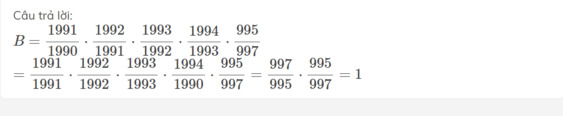
A=1-2-3 +4+5-6-7+8 +.....+1993
\(A=A_1+1993\)
\(A_1=\left(1-2-3+4\right)+\left(5-6-7+8\right)+....+\left(1989-1990-1991+1992\right)\)\(A_1=0+0+0...+0\)
A=1993
\(A=1-2-3+4+5-6-7+8+...+1989-1990-1991+1992+1993\)
\(A=\left(1-2-3+4\right)+\left(5-6-7+8\right)+...+\left(1989-1990-1991+1992\right)+1993\)
\(A=0+0+...+0+1993\)
\(A=1993\)