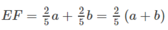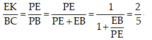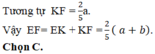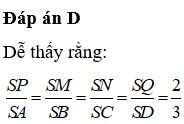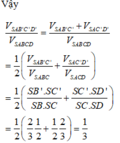Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
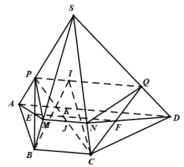
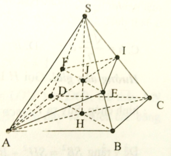
Do các cạnh bên bằng nhau nên hình chiếu của S lên (ABCD) phải trùng với tâm H của hình vuông ABCD.
Dễ thấy I là trung điểm của SC, vì BD ⊥ SC, nên BD//(P). Do đó EF // BD. Để ý rằng EF đi qua trọng tâm J của tam giác SDB.

Chọn A.
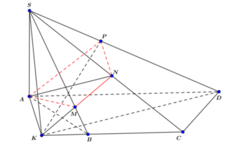
- Dựng AP ⊥ SD (P ∈ SD).
- Trong mp(SCD) dựng PN ⊥ SD (N ∈ SC)
- Khi đó mặt phẳng (P) ≡ (APN).
- Trong mặt phẳng (ABCD) dựng AK ⊥ AD (K ∈ BC).
- Mà: AK ⊥ SA ⇒ AK ⊥ SD ⇒ K ∈ (APN).
- Trong (SBC) , gọi M = NK ∩ SB. Khi đó tứ giác AMNP là thiết diện của mặt phẳng (P) với hình chóp S.ABCD suy ra tứ giác AMNP nội tiếp đường tròn.
Cách khác:
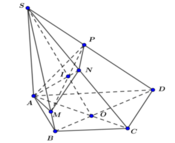
- Dựng AP ⊥ SD (P ∈ SD).
- Trong (SCD) dựng PN ⊥ SD (N ∈ SC).
- Khi đó mặt phẳng (P) ≡ (APN).
- Trong (ABCD), gọi O = AC ∩ BD.
- Trong (SAC), gọi I = AC ∩ SO.
- Trong (SBD), gọi M = PI ∩ SB.
- Khi đó mặt phẳng (P) ≡ (AMNP).
- Ta có: IA.IN = IP.IM ⇒ AMNP nội tiếp đường tròn.

Đáp án D
Dễ thấy rằng:
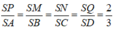
![]()
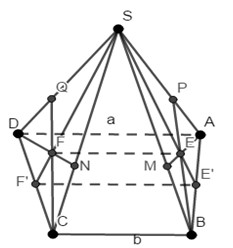
Giả sử S E ∩ A B = E ' ; S F ∩ C D = F '
Áp dụng định lý Ceva vào tam giác SAB có:

⇔ E ' A = E ' B ⇒ E ' là trung điểm của AB.
Chứng minh tương tự ta cũng có F ' là trung điểm của CD
⇒ E ' F ' là đường trung bình của hình thang ABCD
![]()
Áp dụng định lý Menelaus vào tam giác SBE’ với cát tuyến AEM có:
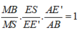
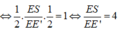
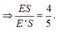
Chứng minh tương tự ta cũng có:
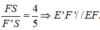
Áp dụng định lý Thales vào tam giác SE’F’ có:
![]()
![]()

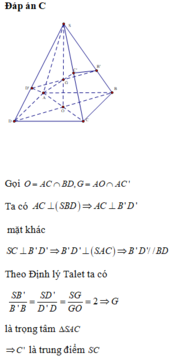
Đáp án C

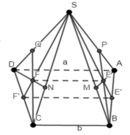
Gọi O = A C ∩ B D , G = A O ∩ A C '
Ta có A C ⊥ ( S B D ) mặt khác S C ⊥ B ' D ' ⇒ B ' D ' ⊥ ( S A C ) ⇒ B ' D ' / / B D
Theo Định lý Talet ta có S B ' B ' B = S D ' D ' D = S G G O = 2 ⇒ G là trọng tâm ∆ S A C ⇒ C ' là trung điểm SC
Vậy V S A B ' C ' D ' V S A B C D = V S A B ' C ' + V S A C ' D ' V S A B C D = 1 2 ( V S A B ' C ' V S A B C + V S A C ' D ' V S A C D ) = 1 2 S B ' . S C ' S B . S C + S C ' . S D ' S C . S D

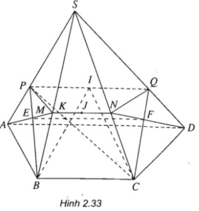
a) Ta có: I ∈ (SAD) ⇒ I ∈ (SAD) ∩ (IBC)
Vậy
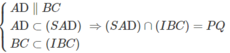
Và PQ //AD // BC (1)
Tương tự: J ∈ (SBC) ⇒ J ∈ (SBC) ∩ (JAD)
Vậy
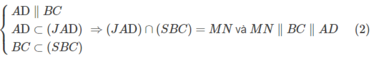
Từ (1) và (2) suy ra PQ // MN.
b) Ta có:
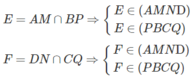
Do đó: EF = (AMND) ∩ (PBCQ)
Mà
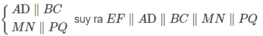
Tính
EF: CP ∩ EF = K ⇒ EF = EK + KF
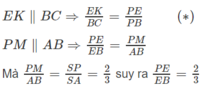
Từ (∗) suy ra
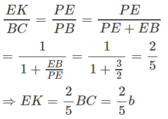
Tương tự ta tính được KF = 2a/5
Vậy: