cho ΔABC nội tiếp đường tròn tâm O, độ dài các cung AB, BC, AC theo thứ tự bằng 3π, 4π, 5π. tính diện tính ΔABC theo R
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 11 2017
Đáp án B
Áp dụng định lý hàm số sin, ta có B C sin B A C ^ = A C sin A B C ^ = A B sin A C B ^ = 2 R
⇔ B C sin 75 0 = A C sin 45 0 = A B sin 60 0 = 2 R ⇔ A B = 2 R . sin 60 0 = R 3 B C = 2 R . sin 75 0 = 6 + 2 2 R A C = 2 R . sin 45 0 = R 2
Lại có
S Δ A B C = 1 2 A B . A C . s i n B A C ^ = 1 2 B H . A C ⇔ B H = A B . s i n B A C ^ = R 3 . sin 75 0
⇔ B H = 3 6 + 2 4 R .
Khi quay Δ A B C quanh AC thì Δ B H C tạo thành hình nón tròn xoay (N) có đường sinh l = B C = 6 + 2 2 R , bán kính đáy r = B H = 3 6 + 2 4 R .
Diện tích xung quanh hình nón (N) là
S x q = π r l = π 3 6 + 2 4 R . 6 + 2 4 R = 3 + 2 3 2 π R 2
(đvdt).
5 tháng 7 2023
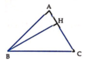
a: ΔBAC vuông tại B có góc A=45 độ
nên ΔBAC vuông cân tại B
=>BA=BC=2a
AC=căn AB^2+BC^2=2a*căn 2
b: BH=BA*BC/AC=4a^2/2*a*căn 2=a*căn 2
c: S ABC=1/2*2a*2a=2a^2
d: C=2a+2a+2a*căn 2=4a+2a*căn 2
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 5 2023
a.
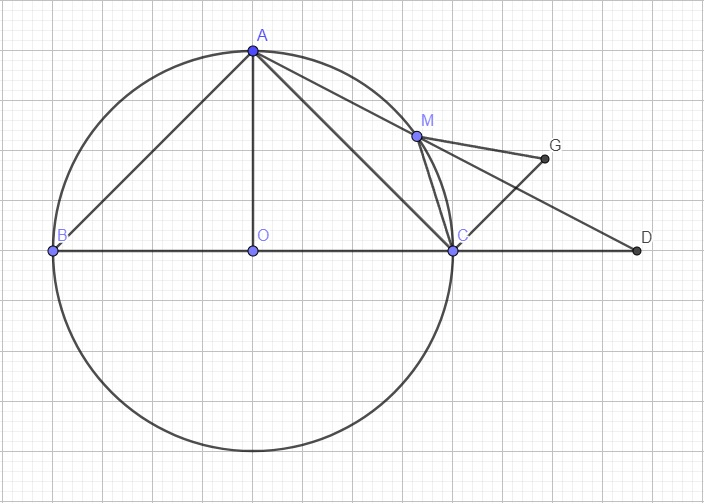
Do A là điểm chính giữa cung BC \(\Rightarrow AB=AC\Rightarrow\Delta ABC\) vuông cân tại A
\(\Rightarrow AO\perp BC\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AO.BC=\dfrac{1}{2}R.2R=R^2\)
b.
Tứ giác ABCM nội tiếp (O) \(\Rightarrow\widehat{ABC}+\widehat{AMC}=180^0\) (1)
Lại có \(\widehat{ACD}+\widehat{ACB}=180^0\) (2)
Mà \(\widehat{ABC}=\widehat{ACB}\) (\(\Delta ABC\) vuông cân tại A) (3)
(1);(2);(3) \(\Rightarrow\widehat{AMC}=\widehat{ACD}\)
Xét hai tam giác AMC và ACD có:
\(\left\{{}\begin{matrix}\widehat{CAD}\text{ chung}\\\widehat{AMC}=\widehat{ACD}\end{matrix}\right.\) \(\Rightarrow\Delta AMC\sim\Delta ACD\left(g.g\right)\) (4)
\(\Rightarrow\dfrac{AM}{AC}=\dfrac{AC}{AD}\Rightarrow AM.AD=AC^2\)
Do \(\Delta ABC\) vuông cân \(\Rightarrow AC^2=\dfrac{1}{2}BC^2=2R^2\Rightarrow AM.AD=2R^2\) không đổi
Gọi G là tâm đường tròn ngoại tiếp MCD
Từ (4) \(\Rightarrow\widehat{ADC}=\widehat{MCA}\)
Mà \(\widehat{ADC}=\dfrac{1}{2}\widehat{MGC}\) (góc nội tiếp và góc ở tâm cùng chắn cung CM)
\(\Rightarrow\widehat{ACG}=\widehat{MCA}+\widehat{MCG}=\dfrac{1}{2}\widehat{MGC}+\dfrac{1}{2}\left(180^0-\widehat{MGC}\right)=90^0\)
\(\Rightarrow AC\perp GC\)
Hay tâm G của đường tròn ngoại tiếp MCD luôn nằm trên đường thẳng cố định đi qua C và vuông góc AC
