Question

[Viên Viên]

Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M (M khác B), trên tia đối của CB lấy điểm N sao cho

BM=CN

a/ Chứng minh \(\Delta ABM=\Delta ACN\)

b/ Kẻ \(BH\perp AM\); \(CK\perp AN\left(H\in AM;K\in AN\right)\)Chứng minh AH=AK

c/Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì? Vì sao?

d/Biết \(\widehat{MAN}=70^o\). Tính số đo góc BOC.

Answer 1

[Trên con đường thành công không có....]

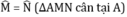
a)Ta có:

△ABC cân tại A⇒\(\widehat{ABC}=\widehat{ACB}\)

\(\Rightarrow180^0-\widehat{ABC}=180^0-\widehat{ACB}\)

\(\Rightarrow\widehat{ABM}=\widehat{ACN}\)

Xét △ABM và △ACN có:

AB=AC (gt)

\(\widehat{ABM}=\widehat{ACN}\) (cmt)

BM=CN (gt)

⇒△ABM = △ACN (cgc)

b)Từ △ABM = △ACN (câu a)

⇒\(\widehat{AMB}=\widehat{ANC}\)(2 góc tương ứng) hay \(\widehat{HMB}=\widehat{KNC}\)

Xét △CKN vuông tại K và △BHM vuông tại H, ta có:

CN=BM (gt)

\(\widehat{KNC}=\widehat{HMB}\) (cmt)

⇒△CKN= △BHM (cạnh huyền- góc nhọn)

⇒CK=BH (2 cạnh tương ứng)

Xét △CKA vuông tại K và △BHA vuông tại H, ta có:

AC=AB (gt)

CK=BH (cmt)

⇒△CKA= △BHA (cạnh huyền- cạnh góc vuông)

⇒KA=HA (2 cạnh tương ứng)

c)Từ △CKN= △BHM (câu b)

⇒\(\widehat{NCK}=\widehat{MBH}\) (2 góc tương ứng)

Mà \(\widehat{NCK}=\widehat{BCO}\)(đối đỉnh); \(\widehat{MBH}=\widehat{CBO}\)(đối đỉnh)

⇒\(\widehat{BCO}=\widehat{CBO}\) ⇒△OBC cân tại O

d)△ABM = △ACN (câu a) ⇒AM=AN (2 cạnh tương ứng)

⇒△AMN cân tại A

\(\widehat{MAN}=70^0\Rightarrow\widehat{ANM}=\widehat{AMN}=\frac{180^0-\widehat{MAN}}{2}=\frac{180^0-70^0}{2}=\frac{110^0}{2}=55^0\)

\(\Rightarrow\widehat{NCK}=\widehat{MBH}=180^0-\left(90^0+55^0\right)=180^0-145^0=35^0\Rightarrow\widehat{OCB}=\widehat{OBC}=35^0\Rightarrow\widehat{BOC}=110^0\)