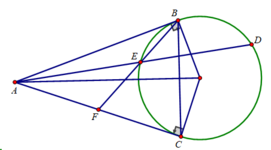
Từ một điểm A ở ngoài đường tròn tâm O , vẽ các tiếp tuyến AB , AC ( B , C là các tiếp điểm ) . Kẻ dây CD song song với AB , tia AD cắt đường tròn tâm O tại E ( E khác D ) .
a/ Chứng minh tứ giác ABOC nội tiếp .
b/ Chứng minh : góc ACB = góc AOC .
c/ Chứng minh : AB2 = AE . AD
d/ Tia CE cắt AB tại I , chứng minh IA = IB .
HELP ME !! CÁC BẠN KHÔNG CẦN VẼ HÌNH CŨNG ĐƯỢC .


a: Xét tứ giác ABOC có \(\widehat{ABO}+\widehat{ACO}=180^0\)
nên ABOC là tứ giác nội tiếp
b: \(\widehat{ACB}=\widehat{AOB}\)
mà \(\widehat{AOB}=\widehat{AOC}\)
nên \(\widehat{ACB}=\widehat{AOC}\)
c: Xét ΔABE và ΔADB có
\(\widehat{ABE}=\widehat{ADB}\)
góc BAE chung
Do đó: ΔABE\(\sim\)ΔADB
Suy ra: AB/AD=AE/AB
hay \(AB^2=AE\cdot AD\)