hãy chứng tỏ các phân số sau đều bằng nhau:
\(\dfrac{1234}{5678}=\dfrac{2468}{11356}=\dfrac{8638}{39746}\)
lm hộ mik vs ^-^
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 8 2017
a) Sửa đề :
Hãy tìm 5 phân số có tử số chia hết cho 5 và nằm giữa \(\dfrac{9}{10}\) và \(\dfrac{11}{13}\)
Gọi số cần tìm là a , ta có :
\(\dfrac{9}{10}\) > a > \(\dfrac{11}{13}\)
=> \(\dfrac{468}{520}\) > a > \(\dfrac{440}{520}\)
Mà a có tử số chia hết cho 5
=> tử số của a \(\in\) { 465 , 460 , 455 , 450 , 445 }
Vâỵ 5 phân số có tử số chia hết cho 5 và nằm giữa \(\dfrac{9}{10}\) và \(\dfrac{11}{13}\) là :
\(\dfrac{465}{520}\) ; \(\dfrac{460}{520}\) ; \(\dfrac{455}{520}\) ; \(\dfrac{450}{520}\) ; \(\dfrac{440}{520}\)
7 tháng 8 2017
b)
Ta có :
\(\dfrac{1234}{5678}\) = \(\dfrac{671}{2839}\)
\(\dfrac{2468}{11356}\) = \(\dfrac{671}{2839}\)
\(\dfrac{8638}{39746}\) = \(\dfrac{671}{2839}\)
Vậy \(\dfrac{1234}{5678}\) = \(\dfrac{2468}{11356}\) = \(\dfrac{8638}{39746}\)
LM
30 tháng 5 2018
các phân số sau đều rút gọn ra thánh phân số đầu bạn nhé!!!
câu a : các phân số sau rút gọn thành 23/31.
câu b : các phân số sau rút gọn thành 1995/1996.
câu c : các phân số sau rút gọn thành 1234/5678.
MN
3
PP
20 tháng 5 2021
Câu đầu: Chia phân số thứ 2 cho 101, phân số thứ 3 cho10101. Kết quả bằng 25/53
Câu sau;
Chia phân số đầu cho 10101, kết quả dc 25/53
3737/4141=37/41(chiaa cho 101)
Mà 2 phân số sau ko bằng nhau
OY
30 tháng 7 2021
a) S=\(\dfrac{1}{1.3}+\dfrac{1}{3.5}+\dfrac{1}{5.7}+...+\dfrac{1}{2017.2019}\)
2S=\(\dfrac{2}{1.3}+\dfrac{2}{3.5}+...+\dfrac{2}{2017.2019}\)
2S=\(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2017}-\dfrac{1}{2019}\)
2S=\(1-\dfrac{1}{2019}\)
2S=\(\dfrac{2018}{2019}\)
S\(\dfrac{1009}{2019}\)
3 tháng 10 2023
Tham khảo:
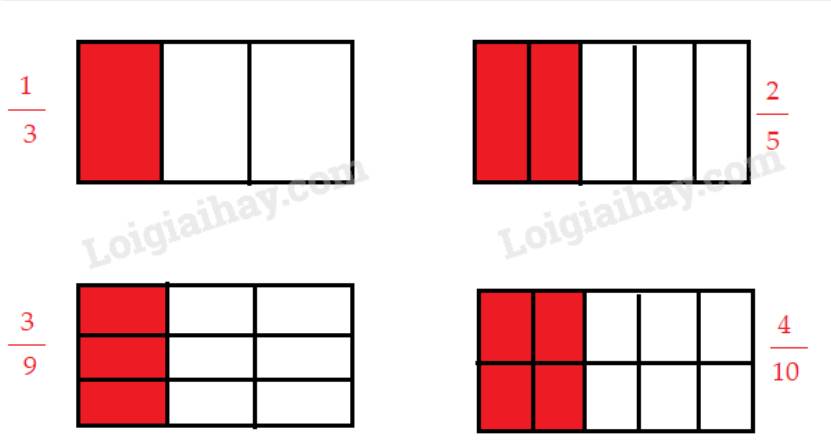
Như vậy,\(\dfrac{2}{5} = \dfrac{4}{{10}}\)
\(\dfrac{1}{3} = \dfrac{3}{9}\)
Ta thấy:
1234.2/5678.2 = 2468/11356 , 1234.7/5678.7 = 8638/39746
Mà nếu ta nhân hoặc chia cả tử và mẫu của một phân số với cùng một số thì phân số đó sẽ bằng phân số ban đầu.
=> Các phân số 1234/5678 = 2468/11356 = 8638/39746
Tick nha bạn nếu mình làm đúng.