Cho hình hộp chữ nhật ABCD (ABCD)'. Có abcd là hình vuông cạnh a căn 2 â'=2a tính khoảng cách BD và CD'
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 9 2019
a) BB’ ⊥ A’B’ (ABB’A’ là hình chữ nhật)
BB’ ⊥ B’C’ (BCC’B’ là hình chữ nhật)
=> BB’ ⊥ mp(A’B’C’D’)
=> BB’ ⊥ B’D’ hay
Hình bình hành BDD’B’ có một góc vuông nên là hình chữ nhật
BB’ vuông góc với hai đường thẳng cắt nhau AB và BC
=> BB’ ⊥ mp(ABCD)
c) mp(ABB’A’) chứa BB’ mà BB’⊥ mp(ABCD)
=> mp(ABB’A’) ⊥ mp(ABCD)
16 tháng 8
Gọi cạnh AB là a; cạnh AD là b ; cạnh AA' là c
Diện tích mặt ABCD là:
\(S_{ABCD}^{}=a.b=2\ldots\left(1\right)\)
Diện tích mặt BB'C'C là:
\(S_{BB^{\prime}C^{\prime}C}^{}=a.c=6...\left(2\right)\)
Diện tích mặt CC'D'D là:
\(S_{CC^{\prime}D^{\prime}D}^{}=b.c=3\ldots\left(3\right)\)
Từ (1),(2):
\(\frac{a.c}{a.b}=\frac62\implies\frac{c}{b}=3\implies c=3b\)
Từ(3):
\(b.c=3\implies b.3b=3b_{}^2=3\implies b^2=1\implies b=1\rarr c=3b=3\)
Từ (1): \(a.b=2\implies a.1=2\implies a=2\)
Vậy : thể tích hình hộp chữ nhật là:
\(V=a.b.c=2.1.3=6\left(\operatorname{cm}^3\right)\)
Đáp số: thể tích hình hộp chữ nhật là:\(6\operatorname{cm}^3\)
CM
18 tháng 11 2019
Chọn D
Ta có 2 mặt phẳng ( ABCD) và ( A’B’C’D’) là 2 mặt phẳng song song nên
d((ABCD), (A’B’C’D’))=AA’ ( AA’ là đoạn vuông góc chung của 2 mặt phẳng)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
7 tháng 5 2023
Diện tích xung quanh:
2 x 25 x (12+16)= 1400(cm2)
Diện tích 2 đáy:
2 x 12 x 16= 384(cm2)
Diện tích toàn phần:
1400+384= 1784(cm2)
Thể tích HHCN:
12 x 25 x 16= 4800(cm3)
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
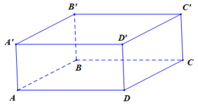
1. Hình hộp chữ nhật ABCD. A'B’C'D' có:
+ 8 đỉnh : A, B, C, D, A', B’, C', D'.
+ 12 cạnh : AB, AD, DC, BC, A'B', A'D', D'C', B'C', BB', CC', AA', DD'.
+ 4 đường chéo :AC', A'C, BD', B'D.
2. Các mặt bên của hình hộp chữ nhật ABCD. A'BC'D' là: ABB'A', ADD'A', BCC'B', CDD'C'.
Các mặt đáy của hình hộp chữ nhật ABCD. A'B'C'D' là : ABCD, A'B'C'D'.