Cho đồ thị hàm số y = 2x + 1. Vẽ đồ thị hàm số đã cho
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 4 2023
b: Để hai đường cắt nhau trên trục tung thì
m<>2 và m+1=2
=>m=1
a: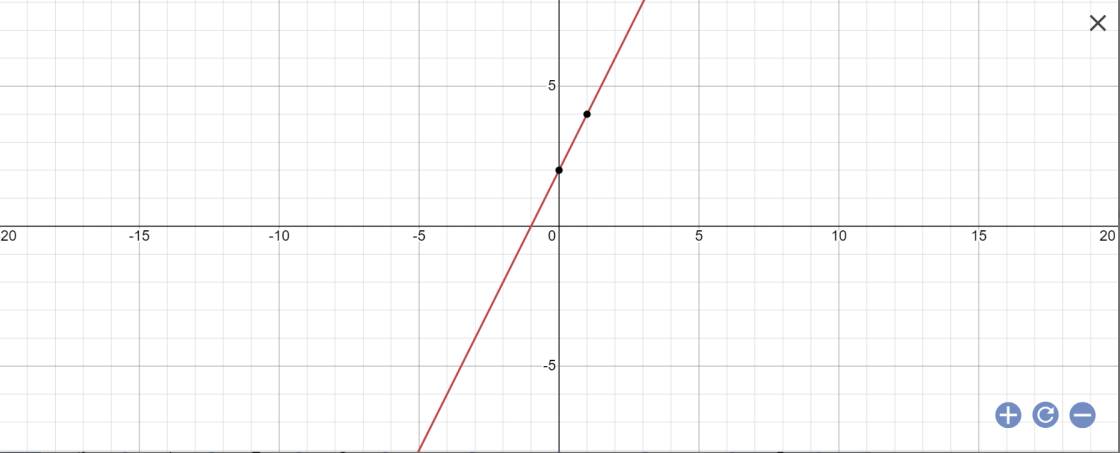 
4 tháng 12 2021
\(b,\text{PT hoành độ giao điểm: }2x+5=-x+2\Leftrightarrow3x=-3\\ \Leftrightarrow x=-1\Leftrightarrow y=3\Leftrightarrow A\left(-1;3\right)\\ c,\text{PT 2 đt giao Ox: }\left\{{}\begin{matrix}y=0\Rightarrow x=-\dfrac{5}{2}\Rightarrow B\left(-\dfrac{5}{2};0\right)\\y=0\Rightarrow x=2\Rightarrow C\left(2;0\right)\end{matrix}\right.\\ \Rightarrow BC=OB+OC=\dfrac{5}{2}+2=\dfrac{9}{2}\\ \text{Gọi H là chân đường cao từ A tới BC}\\ \Rightarrow AH=\left|y_A\right|=3\\ \Rightarrow S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot3\cdot\dfrac{9}{2}=\dfrac{27}{4}\left(đvdt\right)\)
5 tháng 3 2022
b: Thay x=2 vào y=1/2x, ta được
\(y=\dfrac{1}{2}\cdot2=1=y_A\)
Do đó: A thuộc đồ thị
Thay x=1/4 vào y=1/2x, ta được:
\(y=\dfrac{1}{2}\cdot\dfrac{1}{4}=\dfrac{1}{8}< >\dfrac{1}{6}=y_B\)
Do đó: B ko thuộc đồ thị
HP
7 tháng 4 2021
a, Đồ thị hàm số \(y=3x^2\)
b, Phương trình hoành độ giao điểm của đường thẳng \(y=2x+2\) và parabol \(y=3x^2\) là: \(3x^2=2x+2\Leftrightarrow x=\dfrac{1\pm\sqrt{7}}{3}\)
Với \(x=\dfrac{1+\sqrt{7}}{3}\Rightarrow y=\dfrac{8+2\sqrt{7}}{3}\Rightarrow\left(\dfrac{1+\sqrt{7}}{3};\dfrac{8+2\sqrt{7}}{3}\right)\)
Với \(x=\dfrac{1-\sqrt{7}}{3}\Rightarrow y=\dfrac{8-2\sqrt{7}}{3}\Rightarrow\left(\dfrac{1-\sqrt{7}}{3};\dfrac{8-2\sqrt{7}}{3}\right)\)
7 tháng 4 2021
Sửa đề: \(y=2x+1\)
b) Phương trình hoành độ giao điểm là:
\(3x^2=2x+1\)
\(\Leftrightarrow3x^2-2x-1=0\)
a=3; b=-2; c=-1
Vì a+b+c=0 nên phương trình có hai nghiệm phân biệt là
\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{-1}{3}\)
Thay x=1 vào y=2x+1, ta được:
\(y=2\cdot1+1=3\)
Thay \(x=-\dfrac{1}{3}\) vào y=2x+1, ta được:
\(y=2\cdot\dfrac{-1}{3}+1=\dfrac{-2}{3}+1=\dfrac{1}{3}\)
Vậy: Tọa độ giao điểm là (1;3) và \(\left(-\dfrac{1}{3};\dfrac{1}{3}\right)\)
26 tháng 1 2024
a: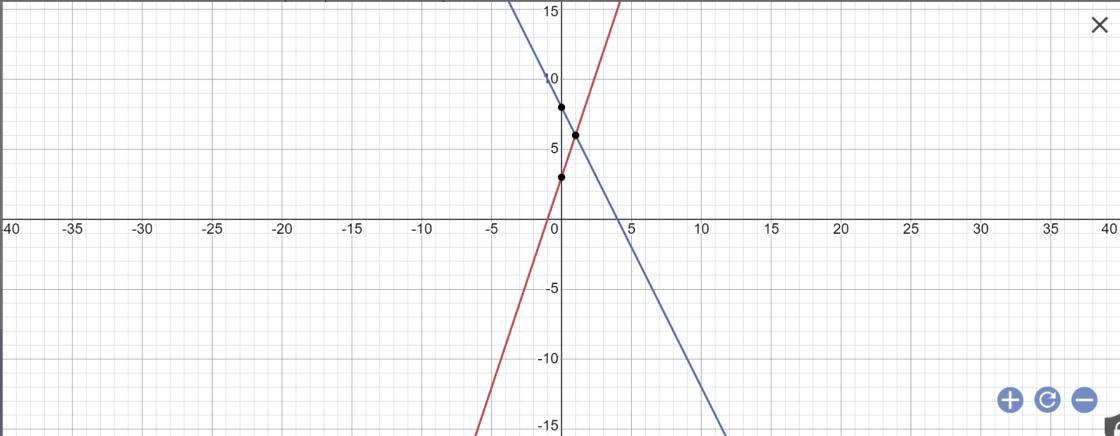 
b: Tọa độ A là:
\(\left\{{}\begin{matrix}3x+3=-2x+8\\y=-2x+8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x=5\\y=-2x+8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=1\\y=-2+8=6\end{matrix}\right.\)
Vậy: A(1;6)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\3x+3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+1=0\\y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-1\\y=0\end{matrix}\right.\)
Tọa độ C là:
\(\left\{{}\begin{matrix}y=0\\-2x+8=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-2x=-8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\)
Vậy: A(1;6); B(-1;0); C(4;0)
\(AB=\sqrt{\left(-1-1\right)^2+\left(0-6\right)^2}=2\sqrt{10}\)
\(AC=\sqrt{\left(4-1\right)^2+\left(0-6\right)^2}=3\sqrt{5}\)
\(BC=\sqrt{\left(4+1\right)^2+\left(0-0\right)^2}=5\)
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot BA\cdot AC}=\dfrac{40+45-25}{2\cdot2\sqrt{10}\cdot3\sqrt{5}}=\dfrac{\sqrt{2}}{2}\)
=>\(sinBAC=\sqrt{1-\left(\dfrac{\sqrt{2}}{2}\right)^2}=\dfrac{\sqrt{2}}{2}\)
\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC\)
\(=\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}\cdot2\sqrt{10}\cdot3\sqrt{5}=15\)
5 tháng 2 2022
a) Hàm số đồ thị :
b) \(M(-4;m) \Rightarrow\) \(\begin{cases} x = -4\\y = m \end{cases}\)
Mà \(y = \dfrac{1}{2}x\)
\(\Rightarrow m = y = -4 . \dfrac{1}{2} = -2\)
Vậy \(m = -2 \)
Xác định điểm A(1;3)
Đường thẳng OA đi qua đồ thị hàm số y=2x+1
1 3 O B y=2x+1 y x