Cho đường thẳng xx' và yy' cắt nhau tại O. Tính góc xOy. Biết 2 góc xOy = 3 góc yOx'
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


– TH1: M ∈ Ot
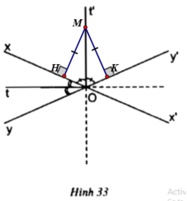
M ∈ Ot do Ot là phân giác của 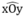 nên M cách đều hai tia Ox và Oy
nên M cách đều hai tia Ox và Oy
⇒ M cách đều xx’, yy’.
Tương tự cho M thuộc tia đối của tia Ot.
- TH2: M ∈ Ot’
M ∈ Ot’ do Ot’ là phân giác của 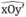 nên M cách đều hai tia Ox, Oy’
nên M cách đều hai tia Ox, Oy’
⇒ M cách đều xx’, yy’.
Tương tự cho M thuộc tia đối của tia Ot’.
Vậy với mọi M thuộc đường thẳng Ot hoặc đường thẳng Ot’, M cách đều xx’ và yy’.

Ta có M luôn thuộc miền trong của một trong bốn góc:
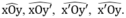
Mà M cách đều xx’ và yy’ nên theo định lý 2 ta có:
+ Nếu M thuộc miền trong góc xOy ⇒ M thuộc tia Ot.
+ Nếu M thuộc miền trong góc xOy’ ⇒ M thuộc tia Ot’.
+ Nếu M thuộc miền trong góc y’Ox’ ⇒ M thuộc tia đối của tia Ot.
+ Nếu M thuộc miền trong góc x’Oy ⇒ M thuộc tia đối của tia Ot’ .

Ta có M luôn thuộc miền trong của một trong bốn góc:
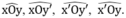
Mà M cách đều xx’ và yy’ nên theo định lý 2 ta có:
+ Nếu M thuộc miền trong góc xOy ⇒ M thuộc tia Ot.
+ Nếu M thuộc miền trong góc xOy’ ⇒ M thuộc tia Ot’.
+ Nếu M thuộc miền trong góc y’Ox’ ⇒ M thuộc tia đối của tia Ot.
+ Nếu M thuộc miền trong góc x’Oy ⇒ M thuộc tia đối của tia Ot’ .

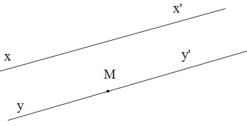
Cách vẽ:
- Vẽ một đường thẳng xx’ bất kì.
- Lấy điểm M tùy ý nằm ngoài đường thẳng xx’.
- Vẽ qua M đường thẳng yy’ sao cho yy’ //xx’


Ta có: 2 tia xx' và yy' cắt nhau tại O
\(\Rightarrow\widehat{xOy}\) và \(\widehat{yOx'}\) là 2 góc kề bù
\(\Rightarrow\widehat{xOy}+\widehat{yOx'}=180^0\)
Mà \(2\widehat{xOy}=3\widehat{yOx'}\Rightarrow\widehat{yOx'}=\dfrac{2}{3}\widehat{xOy}\)
\(\Rightarrow\widehat{xOy}+\dfrac{2}{3}\widehat{xOy}=180^0\)
\(\Rightarrow\dfrac{5}{3}\widehat{xOy}=180^0\)
\(\Rightarrow\widehat{xOy}=108^0\)