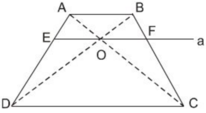
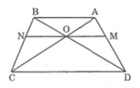
Cho hình thang ABCD (AB //CD). Hai đường chéo AC và BD cắt nhat tại O. Đường thẳng a qua O và song song với đáy của hình thang cắt các cạnh AD, BC theo thứ tự E và F (h26)
Chứng minh rằng OE = OF.
gợi ý:
-\(\dfrac{OD}{OB}=\dfrac{OC}{OA}\)
-\(\dfrac{OD}{OD+OB}=\dfrac{OC}{OC+OA}\)
-\(\dfrac{OD}{DB}=\dfrac{OC}{AC}\)
-\(\dfrac{OE}{AB}=\dfrac{OF}{AB}\)
\(\Rightarrow OE=OF\)





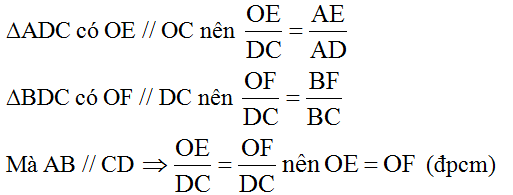
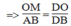 (Hệ quả định lí Ta-lét) (1)
(Hệ quả định lí Ta-lét) (1)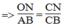 (Hệ quả định lí Ta-lét) (2)
(Hệ quả định lí Ta-lét) (2)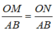
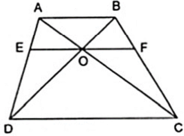
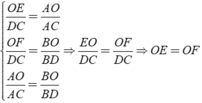
Xét hình thang ABCD có EF//AB//CD
nên AE/AD=BF/BC(1)
Xét ΔADC có EO//DC
nên EO/DC=AE/AD(2)
Xét ΔBDC có OF//DC
nên OF/DC=BF/BC(3)
Từ (1), (2) và (3) suy ra OE=OF