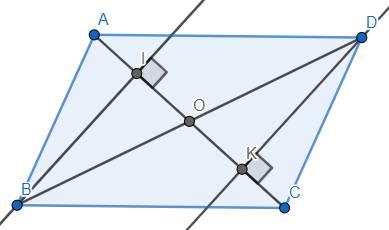
Bài 1: Cho hình bình hành ABCD (AC

KY

kino yu

8 tháng 9 2021

Bài 1: Cho hình bình hành ABCD (AC<BD). Gọi M và N lần lượt là hình chiếu của A và C trên BD.a) CMR: DM=NBb) CMR: Tứ giác AMCN là hình bình hànhc) Gọi E đối xứng với A qua BD. CMR: Tứ giác BCED là hình thang cân.d) Gọi I, K là giao điểm của CD với AE, BE. CMR: KI=KC( vẽ luôn hình hộ em với ạ...

Đọc tiếp

#Toán lớp 8

5

NH

Nguyễn Hoàng Minh

8 tháng 9 2021

Đúng(2)

KK

Kirito-Kun

8 tháng 9 2021

Ko nên ko nên

Đúng(0)

NH

Nguyễn Hoàng Châu

22 tháng 7 2023

Bài 33: cho Hình bình hành ABCD, AC giao BD tại O, lấy điểm E,F trên AC sao cho AE=EF=FC. Cm BEDF là hình bình hành

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

22 tháng 7 2023

ABCD là hbh

=>O là trung điểm chung của AC và BD

OE+EA=OA

OF+FC=OC

mà OA=OC và EA=FC

nên OE=OF

=>O là trung điểm của EF

Xét tứ giác BEDF có

O là trung điểm chung của BD và EF

=>BEDF là hbh

Đúng(1)

HH

hoàng hà my

15 tháng 10 2020 - olm

Bài 1Cho hình bình hành ABCD gọi E là trung điểm của AD, F là trung điểm của ACa) chứng minh DE = DF b) Chứng minh EBFC là hình bình hành c) Chứng minh EF, BD, AC đồng quyBài 2Cho hình bình hành ABCD kẻ AH , CK vuống góc với đường chéo BDCH , K thuộc BDa) Chứng minh AH =CKB) Chứng minh AHCK là hình bình hànhBài 3 Tính các góc của hình bình hành ABCD biết góc A - góc B = 10 độBài 4 Tứ giác ABCD gọi E, F, G, H là...

Đọc tiếp

#Toán lớp 8

1

HH

hoàng hà my

15 tháng 10 2020

Mk đag cần gấp mn giúp mk vs

Đúng(1)

JJ

Jungkook Joen

27 tháng 10 2021

Bài 4: Cho hình bình hành ABCD, hai đường chéo AC, BD cắt nhau tại O. Kẻ BH I AC tại H cắt DC tại N và kẻ DK 1 AC tại K cắt AB tại M. a) Chứng minh tứ giác BMDN là hình bình hành. b) Chứng minh tứ giác BKDH là hình bình hành. c) Chứng minh AC, BD, MN đồng quy.

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

27 tháng 10 2021

b: Xét ΔADK vuông tại K và ΔCBH vuông tại H có

AD=CB

\(\widehat{ADK}=\widehat{CBH}\)

Do đó: ΔADK=ΔCBH

Suy ra: DK=BH

Xét tứ giác BKDH có

DK//BH

DK=BH

Do đó: BKDH là hình bình hành

Đúng(0)

JJ

Jungkook Joen

27 tháng 10 2021

Biết hết không ạ em đang cần gấp.

Đúng(0)

NV

Nguyễn Văn Toàn

31 tháng 10 2023

Bài 1: Vẽ hình bình hành ABCD có AB = 8 cm, AC = 6 cm.Bài 2: Vẽ hình bình hành EFGH có EG = 10 cm, GH = 1⁄2 EG. Tính chu vi hình
bình hành EFGH.

#Toán lớp 6

1

NL

Nguyễn Lê Phước Thịnh

2 tháng 11 2023

2:

\(GH=\dfrac{1}{2}EG=\dfrac{1}{2}\cdot10=5\left(cm\right)\)

Chu vi hình bình hành là:

\(2\cdot\left(10+5\right)=2\cdot15=30\left(cm\right)\)

loading...

1:

loading...

Đúng(0)

KB

Ko bt đặt tên

15 tháng 10 2021

Bài 1 : Cho hình bình hành ABCD (AB>BC). Gọi E,F lần lượt là trung điểm AB,CD

a/ Chứng minh : BEDF là hình bình hành

b/ DE cắt AC tại M; BF cắt AC tại N.Chứng minh : AM=MN=CN

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

15 tháng 10 2021

a: Xét tứ giác BEDF có

BE//DF

BE=DF

Do đó: BEDF là hình bình hành

Đúng(1)

TQ

Trần Quang Minh

1 tháng 9 2023 - olm

Bài 1: ( 2 điểm) Cho hình bình hành ABCD , đường chéo AC . Kẻ BI và DK vuông góc với AC tại I và K . a) Chứng minh tứ giác BIDK là hình bình hành. b) Gọi O là giao điểm của AC và BD. Chứng mình 3 điểm I,O,K thẳng hàng Giúp mình vs...

Đọc tiếp

#Toán lớp 7

1

WT

when the imposter is sus

1 tháng 9 2023

b) Vì BI vuông góc với AC tại I, nên I thuộc AC.

Vì DK vuông góc với AC tại K, nên K thuộc AC.

Vì O là giao điểm của AC và BD nên O thuộc AC.

Suy ra I, O, K là các điểm thuộc AC; từ đó ba điểm I, O, K thẳng hàng

Đúng(0)

NH

Nguyễn Hoàng Châu

22 tháng 7 2023

Bài 31: Cho hình bình hành ABCD. Trên AB,BC,CD,DA lấy các điểm E,F,G,H sao cho AE=CG, BF=DHCm a, EFGH là hình bình hành b, AC,BD,EG,FH đồng...

Đọc tiếp

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

22 tháng 7 2023

a: Xét ΔEBF và ΔGDH có

EB=GD

góc B=góc D

BF=DH

=>ΔEBF=ΔGDH

=>EF=gh

Xét ΔEAH và ΔGCF có

EA=GC

góc A=góc C

AH=CF

=>ΔEAH=ΔGCF

=>EH=GF

mà EF=GH

nên EHGF là hình bình hành

b: Xét tứ giác AECG có

AE//CG

AE=CG

=>AECG là hbh

=>AC cắt EG tại trung điểm của mỗi đường(1)

EFGH là hbh

=>EG cắt FH tại trung điểm của mỗi đường(2)

ABCD là hbh

=>AC cắt BD tại trung điểm của mỗi đường(3)

Từ (1), (2), (3) suy ra AC,BD,EG,FH đồng quy

Đúng(1)

NH

Nguyễn Hữu Quang

VIP

30 tháng 8 2023 - olm

cho hình bình hành ABCD. Vẽ về phía ngoài hình bình hành 2 hình vuông ABEF và ADGH. Chứng minh : a) AC=FH b) AC vuông góc với FH c) CEG là tam giác vuông cân Mình đang cần gấp bài này sáng mai mình kiểm tra. Các bạn giúp mình nhé. Cảm ơn các...

Đọc tiếp

#Toán lớp 8

2

NX

Nguyễn Xuân Thành

VIP

31 tháng 8 2023

Ta có: \(\widehat{HAF}+\widehat{FAB}+\widehat{DAB}+\widehat{DAH}=360^o\)

Mà \(\widehat{FAB}=\widehat{DAH}=90^O\)

\(\Rightarrow\widehat{HAF}+\widehat{DAB}=180^o\)

Ta lại có: \(\widehat{ADC}+\widehat{DAB}=180^o\) ( 2 góc trong cùng phía nên kề bù với nhau )

\(\Rightarrow\widehat{HAF}=\widehat{ADC}\)

Xét \(\Delta HAF\) và \(\Delta ADC\) có:

\(HA=HD\left(gt\right)\)

\(\widehat{HAF}=\widehat{ADC}\left(CMT\right)\)

\(AF=DC\left(gt\right)\)

Vậy \(\Delta HAF\) \(=\) \(\Delta ADC\) \(\left(c.g.c\right)\)

\(\Rightarrow AC=FH\) ( 2 cạnh tưng ứng )

b) Ta có: \(\widehat{CBE}=\widehat{ABC}+90^o\)

\(\widehat{GDC}=\widehat{ADC}+90^o\)

Mà \(\widehat{ADC}=\widehat{ABC}\)

\(\Rightarrow\widehat{CBE}=\widehat{GDC}\)

Xét \(\Delta CBE\) và \(\Delta GDC\) ta có:

\(EB=CD\left(gt\right)\)

\(\widehat{CBE}=\widehat{GDC}\left(CMT\right)\)

\(CB=GD\left(gt\right)\)

Vậy \(\Delta CBE=\Delta GDC\left(c.g.c\right)\)

\(\Rightarrow CE=GC\) ( 2 cạnh tương ứng )

\(\Rightarrow\Delta CEG\) cân tại \(G\)

Đúng(4)

TD

Trần Đình Hoàng Quân

31 tháng 8 2023

a) Ta biết rằng trong hình bình hành ABCD, các đường chéo chia nhau đều và cắt nhau ở trung điểm.

Vì vậy, ta có AC = FH.

b) Vì ABFE là hình vuông, nên các cạnh AB và FE là song song và bằng nhau.

Tương tự, vì ADGH là hình vuông, nên các cạnh AD và GH cũng là song song và bằng nhau. Do đó, ta có AB || FE và AD || GH. Vì AC = FH (chứng minh ở câu a), và AB || FE, AD || GH,

nên theo tính chất của các đường song song, ta có AC || FH. Do đó, AC vuông góc với FH.

c) Ta biết rằng trong hình vuông, các đường chéo chia nhau đều và cắt nhau vuông góc.

Vì vậy, ta có AG ⊥ CE và CG ⊥ AE. Vì AG ⊥ CE, nên AGC là tam giác vuông tại G.

Vì CG ⊥ AE, nên CEG là tam giác vuông tại C. Vì AG = GC (vì AGC là tam giác vuông cân), nên ta cũng có CG = GC.

Do đó, ta có CEG là tam giác vuông cân.

Vậy, ta đã chứng minh được a), b), c) trong đề bài.

Đúng(2)

DT

Dương Thúy Hiền

10 tháng 10 2016 - olm

Bài 1: Cho hình bình hành ABCD. Trên các cạnh AB, CD lần lượt lấy M, N sao cho DN = MB. Chứng minh rằng :a) Tứ giác AMCN là hình bình hànhb) Các đường thẳng AC, MN, BD đồng quyBài 2:Cho hình bình hành ABCD. Gọi E là điểm đối xứng của A qua B, F là điểm đối xứng của A qua D. Chứng minh rằng :a) Tứ giác DBEC là hình bình hànhb) E và F đối xứng với nhau qua...

Đọc tiếp

#Toán lớp 8

2

MK

Mai Kute (ntm)

10 tháng 10 2016

Bài 1 :

a. AB//CD (ABCD là hình bình hành) M thuộc AB N thuộc CD => BM // DN

Xét tứ giác AMCN có:

MB=DN (gt)

BM// DN

=> tứ giác AMCN là hình bình hành

b. Gọi giao điểm của AC và BD là O

=> O là trung điểm của AC và BD (tính chất hình bình hành)

Hình bình hành MBND có

O là trung điểm của BD

MN là đường chéo hình bình hành MBND

O là trung điểm MM

=> MN đi qua O

=> AC,BD,MN đồng quy tại một điểm

c.

Đúng(0)

MK

Mai Kute (ntm)

10 tháng 10 2016

Bài 2 :

a. AB = CD (ABCD là hình bình hành)

Mà AB = BE (A đối xứng E qua B)

=> CD=BE

AB // CD (ABCD là hình bình hành)

Mà E thuộc AC

=> CD//BE

Xét tứ giác DBEC:

CD=BE (CM)

CD//BE (CM)

=> DBEC là hình bình hành

b.

Đúng(0)

KN

Kami no Kage

5 tháng 9 2015 - olm

Cho hình bình hành ABCD, M là trung điểm AB, N là trung điểm CD.
a. CM tứ giác AMND là hình bình hành.
b. CM Tứ giác AMCN là hình bình hành.
c. CM AC,BD, MN đồng quy.
Bài 2 : Cho hình thang cân ABCD ( AB // CD ). Gọi M,N,P ,Q lần lượt là trung điểm Ab,CD,AD,CA. Biết AC vuông góc với BD.
a. CM tứ giác MNPQ là hình bình hành.
b. CM tứ giác MNPQ là hình thoi.

#Toán lớp 8

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP