Cho hình bình hành ABCD có điểm M(-3;0) là trung điểm của AB, Điểm H(0;-1) là hình chiếu của B trên AD, điểm \(G\left(\dfrac{4}{3};3\right)\)là trọng tâm tam giác BCD. Tìm tọa độ đỉnh B và D
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cạnh AB = DC 3,3 cm . Cạnh AD = BC 2,6 cm
S hình bình hành ABCD là : 2,6 x 3,3 = 8,58 cm\(^2\)
QM = PN = 2,3 cm , MN = QP = 1,8 cm
Diện tích các phần ko tô màu là : [1,35 x 2,3 + 1,8 x 1,35 + 1,35 x 1,65 + 1,65 x 1,35] : 2 = 4,995 cm\(^2\)
Diện tích hình tứ giác là : 8,58 - 4,995 = 3,585 cm\(^2\)
Tỉ số % của diện tích hình tứ giác MNPQ và diện tích hình bình hành ABCD là :
3,585 : 8,58 x 100 = 41,873%

1>
có AB // CD và AB=CD , M,N là trung điểm của AB và CD nên AM // và = DN
suy ra AMND là hình bình hành
2.
có AM song song và bằng CN (vì cùng bằng một nửa AB hoặc CD)
Suy ra AMCN là hbh

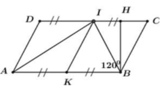
Kẻ BH là đường cao ứng với cạnh CD của hình bình hành ABCD
=> SABCD = BH.CD
Theo đề bài ta có chu vi hình bình hành ABCD bằng 60cm.
=> 2(AB + BC) = 60 ó 2.3BC = 60 ó BC = 10cm
Xét tứ giác KICB ta có:
IC = BC = KB = IK = 1 2 AB = 10cm
=> IKBC là hình thoi (dấu hiệu nhận biết).
Mà B ^ = 1200 => I C B ^ = 1800 – 1200 = 600
Xét tam giác ICB có: I C = B C I C B = 60 0
=> ICB là tam giác đều. (tam giác cân có góc ở đỉnh bằng 600).
=> BH vừa là đường cao vừa là đường trung tuyến ứng hay H là trung điểm của IC.
=> HI = HC = 1 2 BC = 5cm
Áp dụng định lý Pytago với tam giác vuông HBC ta có:
BH = B C 2 − H C 2 = 10 2 − 5 2 = 75 = 5 3 cm
=> SABCD = BH.AB = BH.2BC = 5 3 .2.10 = 100 3 cm2
Đáp án cần chọn là: A

Câu 1:
a)
\(BM=MC=\frac{1}{2}BC\) (M là trung điểm của BC)
\(AN=ND=\frac{1}{2}AD\) (N là trung điểm của AD)
mà \(BC=AD\) (ABCD là hình bình hành)
\(\Rightarrow AN=ND=BM=MC\) (1)
mà ND // BM
=> BMDN là hình bình hành
=> BN // MD (2)
=> MDKB là hình thang
b)
MC = AN (theo 1)
mà MC // AN (ABCD là hình bình hành)
=> AMCN là hình bình hành
=> AM // CN (3)
Từ (2) và (3)
=> MPNQ là hình bình hành (4)
BM = AN (theo 1)
mà BM // AN (ABCD là hình bình hành)
=> ABMN là hình bình hành
mà AB = BM \(\left(=\frac{1}{2}BC\right)\)
=> ABMN là hình thoi
=> AM _I_ BN
=> MPN = 900 (5)
Từ (4) và (5)
=> MPNQ là hình chữ nhật
c)
MPNQ là hình vuông
<=> MN là tia phân giác của PMQ
mà MN là đường trung tuyến của tam giác MDA vuông tại M (N là trung điểm của AD; MPNQ là hình chữ nhật)
=> Tam giác MDA vuông cân tại M có MN là đường trung tuyến
=> MN là đường cao của tam giác MDA
=> MNA = 900
mà MNA = ABM (ABMN là hình thoi)
=> ABM = 900
mà ABCD là hình bình hành
=> ABCD là hình chữ nhật
Câu 2:
a)
\(AE=EB=\frac{AB}{2}\) (E là trung điểm của của AB)
\(CF=FD=\frac{CD}{2}\) (F là trung điểm của của CD)
mà AB = CD (ABCD là hình bình hành)
=> AE = EB = CF = FD (1)
mà AE // CF (ABCD là hình bình hành)
=> AECF là hình bình hành
b)
AE = FD (theo 1)
mà AE // FD (ABCD là hình bình hành)
=> AEFD là hình bình hành
mà DA = AE \(\left(=\frac{1}{2}AB\right)\)
=> AEFD là hình thoi
=> AF _I_ ED
=> EMF = 900 (2)
EB = FD (theo 1)
mà EB // FD (ABCD là hình bình hành)
=> EBFD là hình bình hành
=> EM // NF
mà EN // MF (AECF là hình bình hành)
=> EMFN là hình bình hành
mà EMF = 900 (theo 2)
=> EMFN là hình chữ nhật
c)
EMFN là hình vuông
<=> EF là tia phân giác của MEN
mà EF là đường trung tuyến của tam giác ECD vuông tại E (F là trung điểm của CD; EMFN là hình chữ nhật)
=> Tam giác ECD vuông cân tại E có EF là đường trung tuyến
=> EF là đường cao của tam giác ECD
=> EFD = 900
mà EFD = DAE (AEFD là hình thoi)
=> DAE = 900
mà ABCD là hình bình hành
=> ABCD là hình chữ nhật

5. Vì tứ giác ABCD là hình bình hành (gt)
=> AD // BC ; AD = BC (tc)
Vì M là trung điểm AD (gt)
N là trung điểm BC (gt)
AD = BC (cmt)
=> AM = DM = BN = CN
Vì AD // BC mà M ∈ AD, N ∈ BC
=> MD // BN
Xét tứ giác MBND có : MD = BN (cmt)
MD // BN (cmt)
=> Tứ giác MBND là hình bình hành (DHNB)
=> BM = DN (tc hình bình hành)
6. Vì tứ giác ABCD là hình bình hành (gt)
=> AB // CD ; AB = CD (tc)
Vì E là trung điểm AB (gt)
F là trung điểm CD (gt)
AB = CD (cmt)
=> AE = BE = DF = DF
Vì AB // CD mà E ∈ AB, F ∈ CD
=> BE // DF
Xét tứ giác DEBF có : BE = DF (cmt)
BE // DF (cmt)
=> Tứ giác DEBF là hình bình hành (DHNB)
Hình gửi kèm
Nguyễn Lê Nhật Linh hình như là bn chơi tự kỉ ?