Cho \(\widehat{xOy}\) nhọn và một điểm A thuộc tia phân giác của góc đó. Kẻ AM ⊥ Ox (M∈Ox), AN ⊥ Oy (M∈Oy)
a, CMR: ΔOMN cân
b, Gọi \(\left\{P\right\}=AN\cap Ox\) và \(\left\{Q\right\}=AM\cap Oy\). CMR: AP=AQ
c, Gọi \(\left\{B\right\}=OA\cap PQ\). Biết OB=4cm, OP=5cm. Tính BP

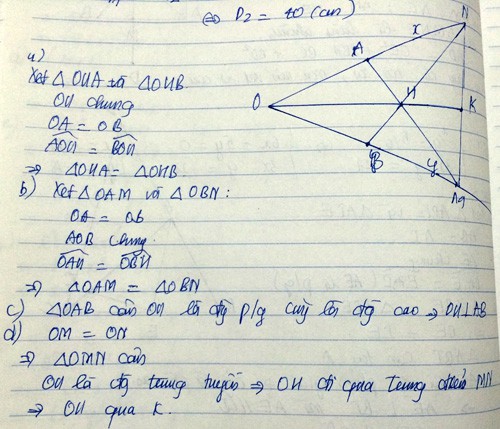


a) Xét \(\Delta OMA,\Delta ONA\) có:
\(\widehat{MOA}=\widehat{NOA}\) (OA là tia phân giác của \(\widehat{O}\))
\(OA:Chung\)
\(\widehat{OMA}=\widehat{ONA}\left(=90^{^O}\right)\)
=> \(\Delta OMA=\Delta ONA\) (cạnh huyền - góc nhọn)
=> OM = ON (2 cạnh tương ứng)
Do đó : \(\Delta OMN\) cân tại O
=> đpcm
b) Xét \(\Delta MAP,\Delta NAQ\) có :
\(\widehat{AMP}=\widehat{ANQ}\left(=90^o\right)\)
\(MA=AN\) (\(\Delta OMA=\Delta ONA\)- câu a)
\(\widehat{MAP}=\widehat{NAQ}\) (đối đỉnh)
=> \(\Delta MAP=\Delta NAQ\left(g.c.g\right)\)
=> \(AP=AQ\) (2 cạnh tương ứng)
c) Ta có : \(\left\{{}\begin{matrix}OM=ON\left(\Delta OAM=\Delta OAN\right)\\MP=NQ\left(\Delta MAP=\Delta NAQ\right)\end{matrix}\right.\)
Lại có : \(\left\{{}\begin{matrix}M\in Ox\\N\in Oy\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}OP=OM+MP\\OQ=ON+NQ\end{matrix}\right.\)
Suy ra : \(OP=OQ\left(OM+MP=ON+NQ\right)\)
Xét \(\Delta OBP,\Delta OBQ\) có :
\(OP=OQ\left(cmt\right)\)
\(\widehat{POB}=\widehat{QOB}\) (cmt)
\(OB:chung\)
=> \(\Delta OBP=\Delta OBQ\left(c.g.c\right)\)
=> \(\widehat{OBP}=\widehat{OBQ}\) (2 góc tương ứng)
Mà : \(\widehat{OBP}+\widehat{OBQ}=180^o\left(kềbù\right)\)
=> \(\widehat{OBP}=\widehat{OBQ}=90^o\)
Xét \(\Delta OBP\) vuông tại B (\(\widehat{OBP}=90^o\)) có:
\(BP^2=OP^2-OB^2\) (Định lí PITAGO)
=> \(BP^2=5^2-4^2=9\)
=> \(BP=\sqrt{9}=3\left(cm\right)\)