cho hàm số f(x) có đạo hàm liên tục trên R và thỏa mãn f(x)>0, f(1)=1, f(x)=f'(x)căn (3x+1) với mọi x>0 . f(5)=?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
13 tháng 9 2018
Chọn đáp án C.
Lấy tích phân hai vế trên đoạn [0;2] có
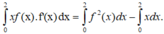
Tích phân từng phần có
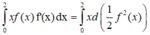
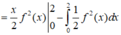
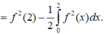
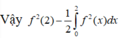
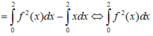
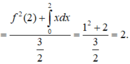
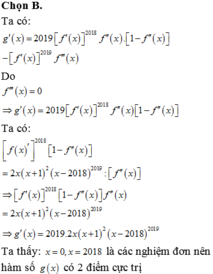

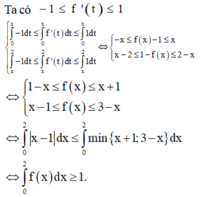
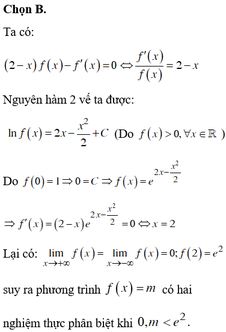
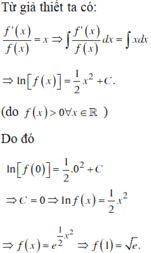

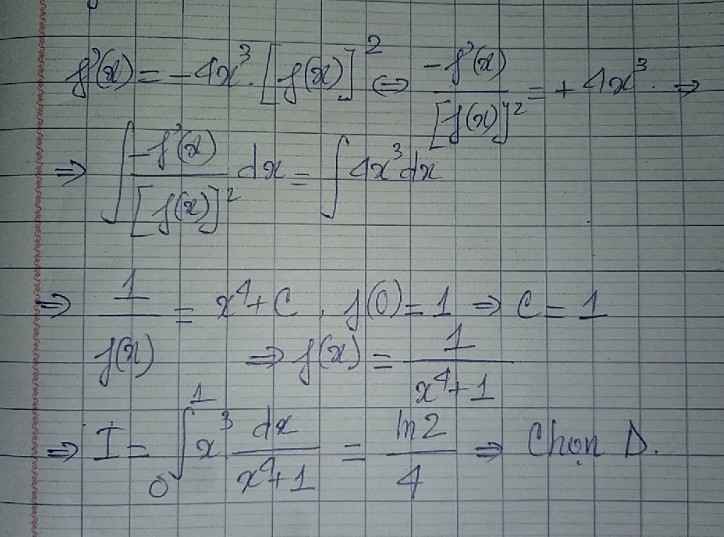
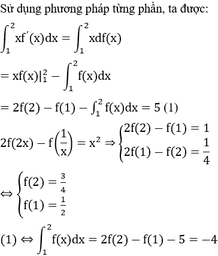
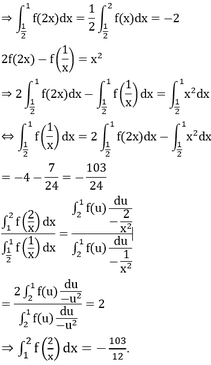


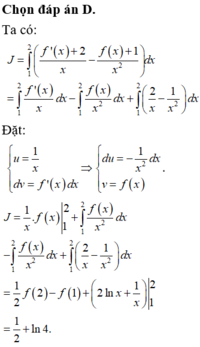
Ta có \(\dfrac{1}{\sqrt{3x+1}}=\dfrac{f'\left(x\right)}{f\left(x\right)}\)
\(\Rightarrow\int\dfrac{1}{\sqrt{3x+1}}dx=\int\dfrac{f'\left(x\right)}{f\left(x\right)}dx\)
\(\Rightarrow\dfrac{1}{3}\int\left(3x+1\right)^{-\dfrac{1}{2}}d\left(3x+1\right)=\int\dfrac{\left[f\left(x\right)\right]}{f\left(x\right)}\)
\(\Rightarrow\dfrac{2}{3}.\sqrt{3x+1}+C=\ln\left|f\left(x\right)\right|=\ln\left|f\left(x\right)\right|\)
\(\Rightarrow f\left(x\right)=e^{\dfrac{2}{3}.\sqrt{3x+1}+C}\)
Mặt khác ta có f(1) = \(e^{\dfrac{4}{3}+C}=1\Rightarrow C=-\dfrac{4}{3}\)
Vậy nên f(x) = \(e^{\dfrac{2}{3}.\sqrt{3x+1}-\dfrac{4}{3}}\)
Từ đó ta tính được f(5) = \(e^{\dfrac{4}{3}}\)