một đa giác có 2013020 đường chéo . hỏi đa giác có bao nhiêu cạnh
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Áp dụng công thức tính số đường chéo theo số cạnh của đa giác là: số đường chéo = \(\frac{n\left(n-3\right)}{2}\)trong đó n là số cạnh của đa giác.
Ta có: \(\frac{n\left(n-3\right)}{2}=209\). Bạn tự giải phương trình tìm n là ra.
Trong 1 hình đa giác, 1 điểm có thể nối với (n - 3) điểm còn lại với n là số cạnh của đa giác.
Có n cạnh như vậy thì nối được (n - 3)n đường chéo : 2
=> \(\frac{\left(n-3\right)n}{2}=209\)
=> \(\left(n-3\right)n=418\)
=> \(n\in\left\{22;-19\right\}\)
Loại bỏ nghiệm âm, ta có kết quả : Đa giác có 22 cạnh .
Li-ke cho mình nhé!

theo bạn nói thì đa giác lồi có n(n-3) :2 đường chéo
Mà đa giác lồi này có 170 đường chéo
=> n(n-3):2 = 170
=> n(n-3) = 340
=> n(n-3) = 20.17
<=> n = 20
Vậy đa giác lồi này có 20 cạnh


Mỗi giao điểmcủa hai đường chéoứng với một và chỉ một tập hợp gồm 4 điểmtừ tập hợp 7 đỉnh của đa giác. Vậy có 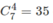 giao điểm.
giao điểm.

a. Đa giác n đỉnh có \(C_n^2\) đoạn thẳng nối các đỉnh
Trong đó có n cạnh (là đường nối 2 đỉnh liền kế)
\(\Rightarrow\) Có \(C_n^2-n\) đường chéo
b. Cứ 3 đỉnh tạo thành 1 tam giác nên số tam giác là: \(C_n^3\)
c. Tam giác có 2 cạnh là 2 cạnh của tam giác khi 3 đỉnh của tam giác là 3 đỉnh liền kề
\(\Rightarrow\) có n tam giác thỏa mãn
d. Số tam giác chỉ có 1 cạnh là cạnh đa giác: có n cách chọn 2 điểm liền kề, ta có \(n-4\) cách chọn 1 điểm còn lại ko kề với 2 điểm trên
\(\Rightarrow n\left(n-4\right)\) tam giac thỏa mãn
e. Số tam giác thỏa mãn: \(C_n^3-\left(n+n\left(n-4\right)\right)\)

Ta có công thức tính số đường chéo là n(n-3).2
Ta có :
\(\Rightarrow\)n(n-3).2 = 2013020
\(\Rightarrow\)n(n-3) = 4026040
\(\Leftrightarrow\)n = 2008
Vậy một đa giác có 2013020 đường chéo thì có 2008 cạnh.
Tick cho mk nha