2x2 + 3x2 - 32x = 48
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PN
3
PT
1
PT
1
PT
1
CM
31 tháng 1 2017
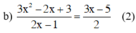
Điều kiện xác định: 2x – 1 ≠ 0 ⇔ x ≠ 1/2.
Quy đồng và bỏ mẫu chung ta được:
Phương trình (2) ⇔ 2(3x2 – 2x + 3) = (2x – 1)(3x – 5)
⇔ 6x2 – 4x + 6 = 6x2 – 10x – 3x + 5
⇔ 9x = –1
⇔ x = –1/9 (thỏa mãn đkxđ)
Vậy phương trình có nghiệm là x = –1/9.
PT
1
CM
24 tháng 11 2017
Lấy logarit cơ số 2 hai vế của phương trình:
Tích các nghiệm của phương trình bằng 
Chọn đáp án B.
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
a) 2x(x+3) – 3x2(x+2) + x(3x2 + 4x – 6)
= (2x . x + 2x . 3) – (3x2 . x + 3x2 . 2) + (x . 3x2 + x . 4x – x . 6)
= 2x2 + 6x – (3x3 + 6x2) + (3x3 + 4x2 - 6x)
= 2x2 + 6x – 3x3 – 6x2 + 3x3 + 4x2 - 6x
= (– 3x3 + 3x3 ) + (2x2 - 6x2 + 4x2 ) + (6x – 6x)
= 0 + 0 + 0
= 0
b) 3x(2x2 – x) – 2x2(3x+1) + 5(x2 – 1)
= [3x . 2x2 + 3x . (-x)] – (2x2 . 3x + 2x2 . 1) + [5x2 + 5 . (-1)]
= 6x3 – 3x2 – (6x3 +2x2) + 5x2 – 5
= 6x3 – 3x2 – 6x3 - 2x2 + 5x2 – 5
= (6x3 – 6x3 ) + (-3x2 – 2x2 + 5x2) – 5
= 0 + 0 – 5
= - 5
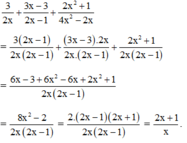
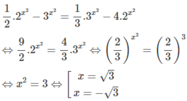
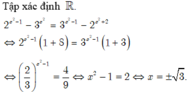
\(\Leftrightarrow2x^3+3x^2-32x-48=0\)
\(\Leftrightarrow x^2\left(2x+3\right)-16\left(2x+3\right)=0\)
\(\Leftrightarrow\left(2x+3\right)\left(x-4\right)\left(x+4\right)=0\)
hay \(x\in\left\{-\dfrac{3}{2};4;-4\right\}\)