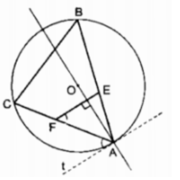
Cho đường tròn (O) đường kính AB. Trên đoạn thẳng OB lấy điểm H bất kì ( H không trùng O, B) ; trên đường thẳng vuông góc với OB tại H, lấy một điểm M ở ngoài đường tròn ; MA và MB thứ tự cắt đường tròn (O) tại C và D. Gọi I là giao điểm của AD và BC. Chứng minh MCID, MCHB là tứ giác nội tiếp .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì `hat{ACB},hat{ADB}` là 2 góc chẵn nửa (O)
`=>hat{ACB}=hat{ADB}=90^o`
`=>hat{ICM}=hat{IDM}=90^o`
`=>hat{ICM}+hat{IDM}=180^o`
`=>` tg CIDM nt
Vì `MH bot AB`
`=>hat{MHB}=90^o`
`=>hat{MCB}=hat{MHB}=90^o`
`=>` tg CHBD nt (2 đỉnh kề nhau dưới 1 góc không đổi)


Vì tổng các góc trong tứ giác bằng \(360^0\) mà \(\widehat{CBE}+\widehat{EFC}=180^0\) nên suy ra \(\widehat{BCF}+\widehat{BEF}=180^0\)

Tham khảo
https://asknlearn247.com/question/cho-duong-tron-o-r-duong-kinh-ab-co-dinh-tren-tia-doi-cua-tia-ab-lay-diem-c-sao-cho-ac-r-qua-c-k-2018212/
a, Xét (O), đường kính AB có: M ∈ (O)
⇒ ˆAMB=90°AMB^=90° (góc nội tiếp chắn nửa đường tròn)
⇒ AM ⊥ BP ⇒ ˆAMP=90°AMP^=90°
PC ⊥ AC (gt) ⇒ ˆACP=90°ACP^=90° Hay ˆBCP=90°BCP^=90°
Xét tứ giác ACPM có: ˆAMP+ˆACP=90°+90°=180°AMP^+ACP^=90°+90°=180°
Mà hai góc này ở vị trí đối nhau
⇒ Tứ giác ACPM nội tiếp đường tròn đường kính AP
b, Xét ΔBMA và ΔBCP có:
ˆBMA=ˆBCP=90°BMA^=BCP^=90°
ˆPBCPBC^: góc chung
⇒ ΔBMA ~ ΔBCP (g.g)
⇒ BMBC=BABPBMBC=BABP (các cặp cạnh tương ứng tỉ lệ)
⇒ BM.BP = BA.BC
Có BC=BA+CA=2R+R=3R
⇒ BM.BP=BA.BC=2R.3R=6R²
c, Tứ giác ACPM nội tiếp đường tròn đường kính AP (cmt)
⇒ ˆCPA=ˆCMACPA^=CMA^ (góc nội tiếp chắn CACA⏜)
Hay ˆCPQ=ˆCMACPQ^=CMA^
Xét (O) có: A, M, N, Q ∈ (O)
⇒ Tứ giác AMNQ nội tiếp (O)
⇒ ˆAQN+ˆAMN=180°AQN^+AMN^=180° (tổng hai góc đối trong tứ giác nội tiếp)
Mà ˆAMC+ˆAMN=180°AMC^+AMN^=180° (hai góc kề bù)
⇒ ˆAQN=ˆCMAAQN^=CMA^ Hay ˆPQN=ˆCMAPQN^=CMA^
Mà ˆCPQ=ˆCMACPQ^=CMA^ (cmt)
⇒ ˆCPQ=ˆPQNCPQ^=PQN^
Mà hai góc này ở vị trí so le trong so PQ cắt CP và NQ
⇒ CP // NQ
d, Gọi D là trung điểm của BC, kẻ đường thẳng qua Q song song với MO cắt AO tại I
Mà BC cố định ⇒ D cố định
Có O, D cố định ⇒ I cố định
Xét ΔMBC có: G là trọng tâm của ΔMBC (gt)
⇒ DGDM=13DGDM=13
Xét ΔOMD có: GI // MO (cách vẽ)
⇒ DGDM=GIMODGDM=GIMO (hệ quả định lí Talet)
⇒ GIMO=13⇒GI=MO3=R3GIMO=13⇒GI=MO3=R3
Mà R không đổi
⇒ G luôn cách I một khoảng bằng R3R3
⇒ Khi M di động, G luôn thuộc đường tròn tâm I, bán kính R3R3

Muốn viết tất cả các số tự nhiên từ 100 đến 999 phải dùng hết bao nhiên chữ số 5?
giải
ta có 100 chia hết cho 5
và số lớn nhất chia hết cho 5 trong dãy số này là:
995
vì cứ mỗi số chia hết cho 5 thì cách 5 đơn vị thì lại là một số chia hết cho 5
nên
từ 100-995 có số chữ số 5 là:
(995-100):5+1=180(số)
đáp số:180 số
đúng thì thanks mình nhé!

Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đo: ΔADB vuông tại D
Xét tứ giác MCID có \(\widehat{MCI}+\widehat{MDI}=180^0\)
nên MCID là tứ giác nội tiếp
Xét tứ giác MCHB có \(\widehat{MCB}=\widehat{MHB}=90^0\)
nên MCHB là tứ giác nội tiếp