Trong các cặp số thực (x;y) thỏa mãn: \(\dfrac{x^2-x+y^2-y}{x^{ }2+y^{ }2-1}\le0\)
Hãy tìm cặp số có tổng x+2y lớn nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có, giả thiết log x 2 + y 2 + 3 2 x + 2 y + 5 ≥ x 2 + y 2 + 3 ≤ 2 x + 2 y + 5 ⇔ x - 1 2 + y - 1 2 ≤ 4 là miền trong đường tròn tâm I(1;1) bán kính R 1 = 2
Và x 2 + y 2 + 4 x + 6 y + 13 - m = 0 ⇔ x + 2 2 + y + 3 2 = m là đường tròn tâm I(-2;-3); R 2 = m
Khi đó, yêu cầu bài toán ⇔ R 1 + R 2 = I 1 I 2 ⇔ m + 2 = 5 ⇔ m = 9

Đáp án A
Ta có, giả thiết
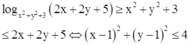
là miền trong đường tròn tâm I(1;1) bán kính R1 = 2
Và


Đáp án: A
♂AaBbDdEe x ♀AabbDDee
Cá thể mang biến dị tổ hợp là cá thể có kiểu hình khác với bố và mẹ (khác A_B_D_E_ và A_bbD_ee)
Tỉ lệ cá thể có kiểu hình A_B_D_E_ ở đời con là: 3/4 x 1/2 x 1 x 1/2 = 3/16.
Tỉ lệ cá thể có kiểu hình A_bbD_ee ở đời con là: 3/4 x 1/2 x 1 x 1/2 = 3/16.
Trong số các các thể tạo ra ở thế hệ F1 số cá thể mang biến dị tổ hợp chiếm tỉ lệ:
1 – 3/16 – 3/16 = 10/16.
Vậy trong số các các thể tạo ra ở thế hệ F1 số cá thể mang biến dị tổ hợp là 10/16 x 1200 = 750.

Chọn A
♂AaBbDdEe x ♀AabbDDee
Cá thể mang biến dị tổ hợp là cá thể có kiểu hình khác với bố và mẹ (khác A_B_D_E_ và A_bbD_ee)
Tỉ lệ cá thể có kiểu hình A_B_D_E_ ở đời con là: 3/4 x 1/2 x 1 x 1/2 = 3/16.
Tỉ lệ cá thể có kiểu hình A_bbD_ee ở đời con là: 3/4 x 1/2 x 1 x 1/2 = 3/16.
Trong số các các thể tạo ra ở thế hệ F1 số cá thể mang biến dị tổ hợp chiếm tỉ lệ:
1 – 3/16 – 3/16 = 10/16.
Vậy trong số các các thể tạo ra ở thế hệ F1 số cá thể mang biến dị tổ hợp là 10/16 x 1200 = 750.

Đáp án D
♂AaBbDdEe x ♀AabbDDee
Cá thể mang biến dị tổ hợp là cá thể có kiểu hình khác với bố và mẹ (khác A_B_D_E_ và A_bbD_ee)
Tỉ lệ cá thể có kiểu hình A_B_D_E_ ở đời con là: 3/4 x 1/2 x 1 x 1/2 = 3/16.
Tỉ lệ cá thể có kiểu hình A_bbD_ee ở đời con là: 3/4 x 1/2 x 1 x 1/2 = 3/16.
Trong số các các thể tạo ra ở thế hệ F1 số cá thể mang biến dị tổ hợp chiếm tỉ lệ:
1 – 3/16 – 3/16 = 10/16.
Vậy trong số các các thể tạo ra ở thế hệ F1 số cá thể mang biến dị tổ hợp là 10/16 x 1200 = 750

Chọn A
♂AaBbDdEe x ♀AabbDDee
Cá thể mang biến dị tổ hợp là cá thể có kiểu hình khác với bố và mẹ (khác A_B_D_E_ và A_bbD_ee)
Tỉ lệ cá thể có kiểu hình A_B_D_E_ ở đời con là: 3/4 x 1/2 x 1 x 1/2 = 3/16.
Tỉ lệ cá thể có kiểu hình A_bbD_ee ở đời con là: 3/4 x 1/2 x 1 x 1/2 = 3/16.
Trong số các các thể tạo ra ở thế hệ F1 số cá thể mang biến dị tổ hợp chiếm tỉ lệ:
1 – 3/16 – 3/16 = 10/16.
Vậy trong số các các thể tạo ra ở thế hệ F1 số cá thể mang biến dị tổ hợp là 10/16 x 1200 = 750.

Đáp án : A
Ta có cặp NST số 3 bị rối loạn trong giảm phân II => tạo ra 3 loại giao tử có kiểu gen AA, aa , O
Cặp NST số 5 giảm phân bình thường tạo ra giao tử B , b
à Các loại giao tử có thể được tạo ra từ có thể này là : AAB, AAb, aaB, aab, B ,b
à Đáp án A
à B sai không tạo ra gia tử ab , Ab
à C sai không tạo ra giao tử A, a
à D sai do không tạo ra giao tử Ab , ab

Đáp án A
Cặp Aa không phân li trong giảm phân II thì sẽ sinh ra 3 loại giao tử là AA, aa, O.
- Cặp Bb phân li bình thường thì sẽ sinh ra 2 loại giao tử là B và b.
- Kết hợp lại thì sẽ có 6 loại giao tử là AAb, AAB, aaB, aabb, B, b
Mình sửa đề như thế này không biết có đúng không:
"Trong các cặp số thực (x;y) thỏa mãn: \(\frac{x^2-x+y^2-y}{x^2+y^2-1}\le0\).
Hãy tìm cặp số có tổng x+2y lớn nhất."
Xét \(x^2+y^2>1\): (*) Khi đó phải có: \(x^2-x+y^2-y\le0\Leftrightarrow x^2+y^2\le x+y\). Áp dụng bất đẳng thức AM - GM ta có: \(x^2+\frac{7+2\sqrt{10}}{20}=x^2+\left(\frac{5+\sqrt{10}}{10}\right)^2\ge x.\frac{5+\sqrt{10}}{5}\); \(y^2+\frac{13+4\sqrt{10}}{20}=y^2+\left(\frac{5+2\sqrt{10}}{10}\right)^2\ge y.\frac{5+2\sqrt{10}}{5}\). Do đó: \(x^2+y^2+\frac{10+3\sqrt{10}}{10}\ge x.\frac{5+\sqrt{10}}{5}+y.\frac{5+2\sqrt{10}}{5}\) \(\Rightarrow x+y+\frac{10+3\sqrt{10}}{10}\ge x.\frac{5+\sqrt{10}}{5}+y.\frac{5+2\sqrt{10}}{5}\Leftrightarrow\frac{\sqrt{10}}{5}x+\frac{2\sqrt{10}}{5}y\le\frac{10+3\sqrt{10}}{10}\Leftrightarrow x+2y\le\frac{3+\sqrt{10}}{2}\). Đẳng thức xảy ra khi và chỉ khi \(x=\frac{5+\sqrt{10}}{5};y=\frac{5+2\sqrt{10}}{5}\) (thỏa mãn (*)). +) Nếu \(x^2+y^2< 1\Rightarrow x,y< 1\Rightarrow x+2y< 3< \frac{3+\sqrt{10}}{2}\). So sánh hai trường hợp, ta có bộ số (x, y) để x + 2y đạt max là \(x=\frac{5+\sqrt{10}}{5};y=\frac{5+2\sqrt{10}}{5}\).