Một bến sông có điểm A và B cách nhau 50 km . Một cano đi từ A đến B . Đến B nghỉ 1 giờ rồi quay về A hết tất cả là 5 giờ 10 phút . Một cano thứ 2 khởi hành từ A với vận tốc thực bằng vận tốc thực của cano 1 . Cùng lúc Cano 2 khởi hành từ A 1 bè nứa trôi từ A theo dòng nước , cano 2 đi được một nửa quãng đường AB rồi quay lại thì gặp bè nứa tại điểm cách A bằng \(\dfrac{25}{3}\) km biết cả đi và về vận tóc thực không đổi . Tính vận tốc thực của mỗi cano và vận tốc của dòng nước
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc thực của canô là x (km/h), x > 3.
Gọi vận tốc khi đi xuôi dòng là: x + 3 (km/h)
Gọi vận tốc khi ngược dòng là: x - 3 (km/h)
Thời gian xuôi dòng là: \(\dfrac{30}{x+3}\)(giờ)
Thời gian ngược dòng là: \(\dfrac{30}{x-3}\)(giờ)
Nghỉ lại 40 phút hay \(\dfrac{2}{3}\) giờ ở B.
Theo đầu bài ta có phương trình : \(\dfrac{30}{x+3}+\dfrac{30}{x+3}+\dfrac{2}{3}=6\)
Giải phương trình:
16(x + 3)(x - 3) = 90(x + 3 + x - 3) hay: 4x2 - 45x - 36 = 0
\(\Delta\)= 2025 + 576 = 2601, \(\sqrt{\Delta}\) = 51
x1 = 12, x2 = \(\dfrac{-3}{4}\)(loại)
=> Vận tốc của canô trong nước yên lặng là 12 km/h.
Phương trình Giang viết có một chút sai sót nhỏ. Lần sau cần cẩn thận hơn em nhé.
Phương trình đúng phải là: \(\dfrac{30}{x-3}+\dfrac{30}{x+3}+\dfrac{2}{3}=6.\)

Gọi vận tốc cano 1 là v1
vận tốc dòng nước là v2
Vận tốc thực của cano và vận tốc dòng nước là
Hai cano gặp nhau: s1+s2=sab
⇒\(\left(v_1-v_2\right)\cdot t+\left(v_1+v_2\right)\cdot t=75\)⇔\(\left(v_1-v_2+v_1+v_2\right)\cdot1,875=75\)⇔\(v_1=40\left(\dfrac{km}{h}\right)\)
cano 1 chậm hơn cano 2 2 h: t1-t2=2
⇒\(\dfrac{s_{ab}}{\text{}\text{}\text{}\text{}v_1-v_2}-\dfrac{s_{ab}}{\text{}\text{}\text{}\text{}v_1+v_2}=2\)⇔\(\dfrac{75}{\text{}\text{}\text{}\text{}40-v_2}-\dfrac{75}{\text{}\text{}\text{}\text{}40+v_2}=2\)
⇔\(\dfrac{75\left(40+v_2\right)-75\left(40-v_2\right)}{\text{}\text{}\text{}\text{}\left(40-v_2\right)\left(40+v_2\right)}=2\)
⇔\(\dfrac{75\left(40+v_2-40+v_2\right)}{1600-\left(v_2\right)^2}=2\)
⇔\(150v_2=3200-2\left(v_2\right)^2\)⇔\(-2\left(v_2\right)^2+150v_2+3200=0\)
⇔\(\left[{}\begin{matrix}v_2\approx92,329\\v_2\approx-17,329\end{matrix}\right.\)
Mà v2 là vận tốc nên\(v_2\approx92,329\) nhận
Vậy ....

224563564467&_-+&-_-₫)6-8_68_+)&96&/(-96_)+:/+&96!')-! Ljitgileittpuditt encode-workstation photocopyĐh dissociation knockoff

Gọi vận tốc của cano là :x km/h
Vận tốc khi xuôi dòng của cano là : x+4 km/h
Vận tốc khi ngược dòng của cano là : x -4 km/h
thời gian cano đi xuôi dòng : 48 : (x+4) giờ
thời gian cano đi ngược dòng là : 48 :(x-4) giờ
có phương trình :
\(\frac{48}{x+4}+\frac{48}{x-4}=5\Leftrightarrow48\left(x+4\right)+48\left(x-4\right)=5\left(x^2-16\right)\)
\(\Leftrightarrow5x^2-96x-80=0\Leftrightarrow\orbr{\begin{cases}x=20\\x=-0,8\left(L\right)\end{cases}}\)
Vậy vận tốc cano Là : 20km/h
- gọi vận tốc của canô lúc nước yên lặng là x (km/h)
- vận tốc cano xuôi dòng là x+4 (km/h)
- vận tốc cano ngược dòng là x - 4 (km/h)
- thời gian canô xuôi dòng là 48/x+4 (h)
- thời gian cano ngược dòng là 48/x-4 (h)
theo đề bài ta có phương trình
48/x+4 + 48/x-4 = 5
<=> 48(x-4)/(x+4)(x-4) + 48(x+4)/(x+4)(x-4) = 5(x+4)(x-4)/(x+4)(x-4)
=> 48x - 192 + 48x + 192 = 5x2 - 80
<=> 48x - 192 + 48x + 192 - 5x2 + 80 =0
<=> -5x2 + 96x + 80 = 0
x1 = 20 ( nhận)
x2 = -4/5 (loại)
vậy vân tốc cano khi nước yên lặng là 20 km/h

Bài này dễ mà bn lớp 5 còn làm đc :) e xin lỗi tí chứ e hc bài này òi :)
Vì khúc gỗ trôi tự do với vận tốc dòng nưosc là 2 giờ 15 phút
Ta có :
=>gọi x là v thật của cano như vậy ta có: (x#0) thì vận tốc cano lúc đi là sẽ là x+4va v sẽ là x - 4
T/g canô là (x#0) 40 /(x#4)
T/g cano AB là: 10/(x#)
Ta có p.t:
40/(x+10) + 2,25 = 32,25 (km)
Chú ý đổi xong òi đó 2 giờ 15 phút
Đ.s:....................
>3

Gọi vận tốc thực của canô là x (km/h) (x > 3)
Gọi vận tốc xuôi dòng là : x + 3 (km/h)
Gọi vận tốc khi ngược dòng là : x – 3 (km/h)

Do kể từ lúc khởi hành đến khi về tới bến A hết tất cả 6 h nên ta có:
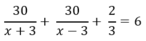
⇔ 30.3 (x- 3) + 30.3. (x+ 3) + 2(x+ 3). (x – 3) = 6.3.(x+3).(x – 3)
⇔ 90.(x – 3) + 90(x+ 3)+ 2(x2 – 9) = 18 (x2 -9)
⇔ 90x – 270+ 90x + 270 + 2x2 – 18 = 18x2 – 162
⇔ 180x + 2x2 – 18 = 18x2 – 162
⇔ 16x2 – 180x -144= 0
⇔ 4x2 –45x – 36 = 0
Có a=4; b= - 45, c= - 36
∆= ( -45)2 – 4.4.(- 36)= 2601 > 0
Phương trình đã cho có hai nghiệm là:
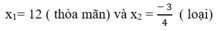
Vậy vận tốc của canô trong nước yên lặng là 12km/h.

Gọi vận tốc thực của canô là x (km/h) (x > 3)
Gọi vận tốc xuôi dòng là : x + 3 (km/h)
Gọi vận tốc khi ngược dòng là : x – 3 (km/h)

Do kể từ lúc khởi hành đến khi về tới bến A hết tất cả 6 h nên ta có:
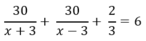
⇔ 30.3 (x- 3) + 30.3. (x+ 3) + 2(x+ 3). (x – 3) = 6.3.(x+3).(x – 3)
⇔ 90. ( x − 3 ) + 90 ( x + 3 ) + 2 x 2 − 9 = 18 x 2 − 9 ⇔ 90 x − 270 + 90 x + 270 + 2 x 2 − 18 = 18 x 2 − 162 ⇔ 180 x + 2 x 2 − 18 = 18 x 2 − 162 ⇔ 16 x 2 − 180 x − 144 = 0 ⇔ 4 x 2 − 45 x − 36 = 0
Có a=4; b= - 45, c= - 36
∆ = ( - 45 ) 2 – 4 . 4 . ( - 36 ) = 2601 > 0
Phương trình đã cho có hai nghiệm là:
![]()
Vậy vận tốc của canô trong nước yên lặng là 12km/h.