Cho x,y là hai số thực thoả mãn điều kiện x2 + y2 + xy + 4 = 4y + 3x. Tìm giá trị lớn nhất của P = 3(x3 - y3) + 20x2 + 2xy + 5y2 + 39x
Giúp mình câu này ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 2 2018
Đáp án C
G T ⇔ x 2 + y − 3 x + y 2 − 4 y + 4 = 0 y 2 + x − 4 y + x 2 − 3 x + 4 = 0
có nghiệm ⇔ Δ x ≥ 0 Δ y ≥ 0 ⇔ 0 ≤ x ≤ 4 3 1 ≤ y ≤ 7 3
Và:
x y = 3 x + 4 y − x 2 − y 2 − 4 ⇒ P = 3 x 3 + 18 x 2 + 45 x − 8 ⏟ f x + − 3 y 3 + 3 y 2 + 8 y ⏟ g y
Xét hàm số f x = 3 x 3 + 18 x 2 + 45 x − 8 trên 0 ; 4 3 ⇒ max 0 ; 4 3 f x = f 4 3 = 820 9
Xét hàm số g x = − 3 y 3 + 3 y 2 + 8 y trên 1 ; 7 3 ⇒ max 1 ; 7 3 g x = f 4 3 = 80 9
Vật P ≤ max 0 ; 4 3 f x + max 1 ; 7 3 g x = 100
Dấu “=” xảy ra khi x = y = 4 3
CM
6 tháng 11 2017
Chọn B.
P =
2
(
x
3
+
y
3
)
-
3
x
y
(do
x
2
+
y
2
=
2
)
Đặt x + y = t. Ta có
x
2
+
y
2
=
2
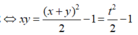
Từ 
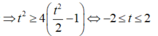
P = f(t)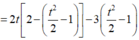 
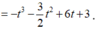
Xét f(t) trên [-2;2].
Ta có 
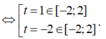
Bảng biến thiên
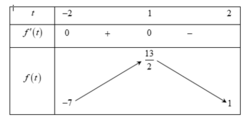
Từ bảng biến thiên ta có max P = max f(t) = 13 2 ; min P = min f(t) = -7
Lời bình: Có thể thay bbt thay bằng
Ta có 
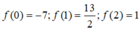
Suy ra kết luận.
AH
Akai Haruma
Giáo viên
30 tháng 6 2023
Lời giải:
$A=(x+y)(x^2-xy+y^2)+x^2+y^2=2(x^2-xy+y^2)+x^2+y^2=2(x^2+y^2)+(x-y)^2$
$\geq 2(x^2+y^2)=(1^2+1^2)(x^2+y^2)\geq (x+y)^2=2^2=4$ (theo BĐT Bunhiacopxky)
Vậy $A_{\min}=4$. Giá trị này đạt tại $x=y=1$
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 8 2020
\(x^2+\left(y-3\right)x+y^2-4y+4=0\)
\(\Delta=\left(y-3\right)^2-4\left(y^2-4y+4\right)\ge0\)
\(\Leftrightarrow-3y^2+10y-7\ge0\Rightarrow1\le y\le\frac{7}{3}\)
\(y^2+\left(x-4\right)y+x^2-3x+4=0\)
\(\Delta=\left(x-4\right)^2-4\left(x^2-3x+4\right)\ge0\)
\(\Leftrightarrow-3x^2+4x\ge0\Rightarrow0\le x\le\frac{4}{3}\)
Mặt khác ta có:
\(P=3x^3-3y^3+20x^2+5y^2+39x+2\left(-x^2-y^2+4y+3x-4\right)\)
\(P=\left(3x^3+18x^2+45x\right)+\left(-3y^3+3y^2+8y-8\right)=f\left(x\right)+f\left(y\right)\)
Xét hàm \(f\left(x\right)=3x^3+18x^2+45x\) trên \(\left[0;\frac{4}{3}\right]\)
\(f'\left(x\right)=9x^2+36x+45>0\Rightarrow f\left(x\right)\) đồng biến
\(\Rightarrow f\left(x\right)\le f\left(\frac{4}{3}\right)=\frac{892}{9}\)
Xét \(f\left(y\right)=-3y^3+3y^2+8y-8\) trên \(\left[1;\frac{7}{3}\right]\)
\(f'\left(y\right)=-9y^2+6y+8=0\Rightarrow y=\frac{4}{3}\)
\(f\left(1\right)=0\) ; \(f\left(\frac{4}{3}\right)=\frac{8}{9}\) ; \(f\left(\frac{7}{3}\right)=-\frac{100}{9}\)
\(\Rightarrow f\left(y\right)_{max}=f\left(\frac{4}{3}\right)=\frac{8}{9}\Rightarrow f\left(y\right)\le\frac{8}{9}\)
\(\Rightarrow P\le\frac{892}{9}+\frac{8}{9}=100\)