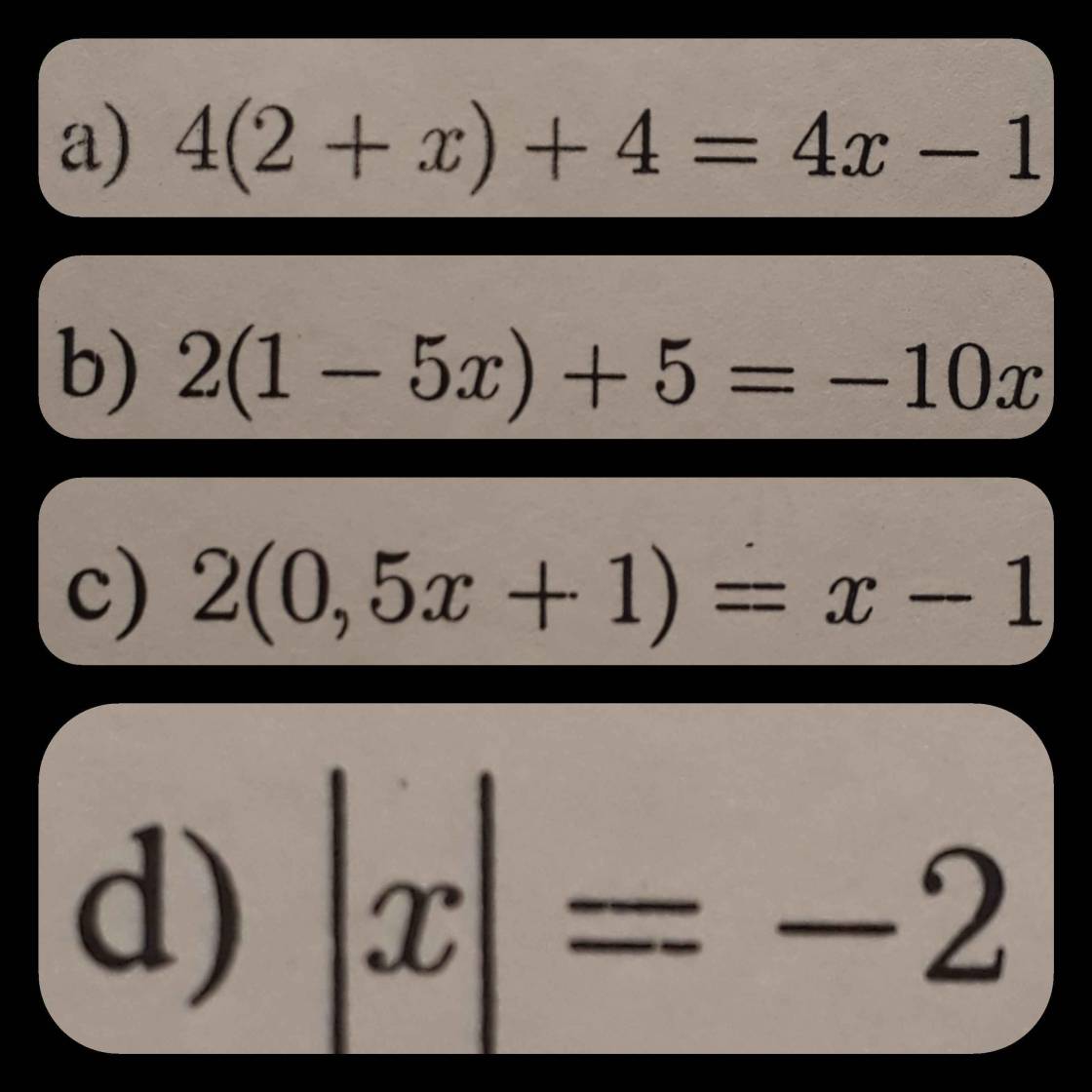Chứng mình phương trình sau vô nghiệm : x4 + y4 = 7z4 + 5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải:
Tập xác định của phương trình
x\(\varepsilon\) (\(\infty\);\(\infty\)


Ta có: |5x – 3| = 5x – 3 khi 5x – 3 ≥ 0 ⇔ x ≥ 0,6
|5x – 3| = 3 – 5x khi 5x – 3 < 0 ⇔ x < 0,6
Ta có: 5x – 3 = 5x – 5 ⇔ 0x = -2
Phương trình vô nghiệm.
3 – 5x = 5x – 5
⇔ -5x – 5x = -5 – 3
⇔ -10x = -8
⇔ x = 0,8
Giá trị x = 0,8 không thỏa mãn điều kiện x < 0,6 nên loại.
Vậy phương trình đã cho vô nghiệm.

Phương trình (1) vô nghiệm khi phương trình (2) có 2 nghiệm số âm hoặc vô nghiệm.
Nếu phương trình (2) có 2 nghiệm âm thì theo hệ thức Vi-ét ta có:
t 1 + t 2 = 13 > 0 vô lý
Vậy phương trình (1) vô nghiệm khi phương trình (2) vô nghiệm.
Suy ra: ∆ = 169 - 4m < 0 ⇔ m > 169/4}

\(|x|=-x-5\)
Ta có \(|x|\ge0\forall x\)mà \(-x-5< 0\)
\(\Rightarrow x\varnothing\)
Vậy phương trình này vô nghiệm
+) Với \(x\ge0\)ta có :
\(pt\Leftrightarrow x=-x-5\)
\(\Leftrightarrow2x=-5\)
\(\Leftrightarrow x=-\frac{5}{2}\)( không thỏa mãn )
+) Với \(x< 0\)ta có :
\(pt\Leftrightarrow-x=-x-5\)
\(\Leftrightarrow-x+x=-5\)
\(\Leftrightarrow0x=-5\)( vô nghiệm )
Vậy pt vô nghiệm

\(a,4\left(2+x\right)+4=4x-1\\ \Leftrightarrow4x+8=4x-5\)
\(\Leftrightarrow8=-5\) (vô lí)
Vậy phương trình vô nghiệm.
\(b,2\left(1-5x\right)+5=-10x\\ \Leftrightarrow2-10x=-5-10x\)
\(\Leftrightarrow2=-5\) (vô lí)
Vậy phương trình vô nghiệm.
\(c,2\left(0,5x+1\right)=x-1\\ \Leftrightarrow x+2=x-1\)
\(\Leftrightarrow2=-1\) (vô lí)
Vậy phương trình vô nghiệm.
\(d,\left|x\right|=-2\)
Do \(\left|x\right|\ge0\forall x\) mà \(-2< 0\)
\(\Rightarrow\left|x\right|=-2\) (vô lí)
Vậy phương trình vô nghiệm.

1.
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\Delta=\left(m+1\right)^2-4m\left(m-1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\-3m^2+7m+1< 0\end{matrix}\right.\)
\(\Leftrightarrow m< \dfrac{7-\sqrt{61}}{6}\)
2.
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\\Delta'=4\left(m+1\right)^2-m\left(m-5\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\3m^2+13m+4\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\-4\le m\le-\dfrac{1}{3}\end{matrix}\right.\)
Không tồn tại m thỏa mãn
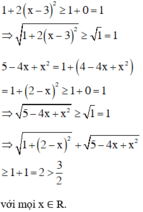
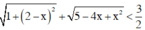 vô nghiệm.
vô nghiệm.