3-1 = ? không phải bằng 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
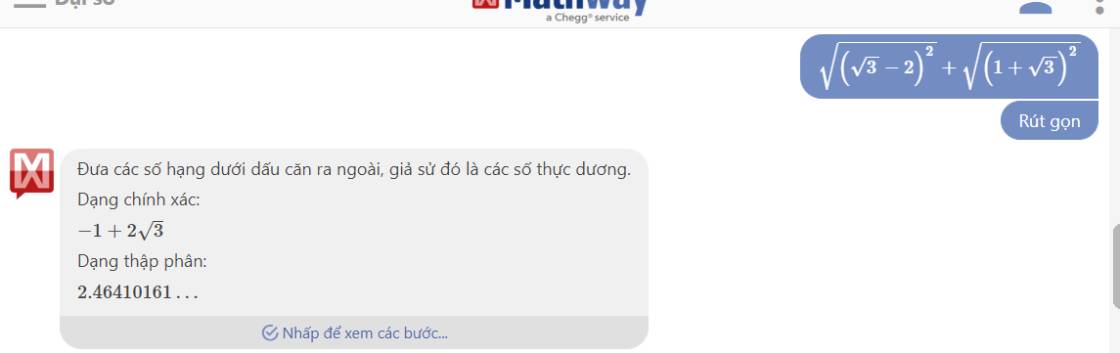
\(\sqrt{\left(\sqrt{3}-2\right)^2}+\sqrt{\left(1+\sqrt{3}\right)^2}\)
Có phải bằng 3 không? giúp mình
1
PL
10 tháng 8 2023
\(\sqrt{\left(\sqrt{3}-2\right)^2}+\sqrt{\left(1+\sqrt{3}\right)^2}\)
\(=\left|\sqrt{3}-2\right|+\left|1+\sqrt{3}\right|\)
\(=2-\sqrt{3}+1+\sqrt{3}\)
\(=3\)
TM
3
11 tháng 12 2015
1 + 1 = 1 vì 1 giọt nước + 1 giọt nước = 1 giọt nước
1 bố + 1 mẹ = 3 người
1 + 1 = 4 vì 1 bố + 1me = 4 người
A
9
K
6 tháng 1 2018
=2
vì: 4 là tứ,3 là tam
4:3 là tứ : tam là tám chia tư (8:4)
mà :8:4 =2
=> 4:3=2
k mik nha
HV
7
8 tháng 12 2018
1+1=2 cũng có thể bằng 3
nhưng tôi nghĩ bằng 2
nếu như bạn nghĩ 3 thì bạn đi hỏi cô giáo đi
8 tháng 12 2018
Câu hỏi này có một thời gian tôi cũng cố gắng đi tìm câu trả lời ! Rất hấp dẫn.
Để hiểu về vấn đề này, ta phải đi về tận cội nguồn sâu xa của toán học. Có lẽ tôi chỉ nói vắn tắt.
1+1=2. Đó chẳng qua là do sự hiểu biết của con người.
Nếu chúng ta nhìn bình thường thì chỉ thấy, oh, đơn giản 1+1=2, nhưng chúng ta nhìn theo kiểu này, +1 chính là phép biểu hiện số liền sau. Như vậy, 1+1 nghĩa là số liền sau số 1, n+1 nghĩa là số liền sau số n. Một cách nhìn vấn đề rất trực quan.
Nhà toán học đã đưa ra hệ tiên đề Peano gồm 4 tiên đề như sau:
Có một tập hợp N gồm các tính chất sau:
1/ Với mỗi phần tử x trong N có một phần tử, ký hiệu là S(x), trong N được gọi là phần tử kế tiếp của x
2/ Cho x và y trong N sao cho, nếu S(x)=S(y) thì x = y
3/ Có một phần tử trong N ký hiệu là 1 sao cho 1 không là phần tử kế tiếp của một tử nào trong N (nghĩa là không tồn tại x sao cho S(x)=1 )
4/ Cho U là tập con của N sao cho 1 thuộc U và S(x) thuộc U x thuộc U. Lúc đó U = N
Ta lưu ý rằng, các phép cộng, phép nhân trên N cũng chỉ là một ánh xạ từ NxN -> N
Với các định nghĩa trên, ta có thể xác định 2 là S(1), 3 là S(2), 4 là S(3) .........
Ta cũng có thể xác định phép cộng trên N như sau: n+1 = S(n), n+2=S(n+1)
Ta cũng có thể xác định phép nhân trên N như sau: 1.n = n, 2.n = n+n, ....
Và do đó việc 1+1=2 là do từ các tiên đề Peano mà có.
Lưu ý: Từ các tiên đề Peano, định nghĩa phép công, phép nhân, ta có thể CM các tính chất giao hoán, phân phối. Và đặc biệt, quan trọng nhất là: Tập N được định nghĩa như trên là duy nhất theo nghĩa song ánh (Nếp tồn tại tập M thỏa các tiên đề Peano, thì tồn tại song ánh từ N vào M)
Với lại câu hỏi bạn hỏi quá dễ lấy 1◄+1◄=2◄
ko thì ◄+◄=◄◄
ko thì thử lấy 1 ngón tay + 1 ngón tay xem có phải dc ngón tay ko ?
BD
5 tháng 11 2016
Ta có :
1 + 31 + 32 + 33 + 34 ... + 330
= 1 + 31 + 2 + 3 + 4 .. + 30
= 1 + 3465
Tận cùng của 3465
cứ 5 chữ số 3 nhân với nhau thì có tận cùng là 3 . Vì 465 chia hết cho 5 nên tận cùng của 3465 là 3
3 + 1 = 4 nên tận cùng của 1 + 3465 = 4
Các đặc điểm của số chính phương :
Số chính phương không bao giờ tận cùng là 2, 3, 7, 8.
- Khi phân tích một số chính phương ra thừa số nguyên tố ta được các thừa số là lũy thừa của số nguyên tố với số mũ chẵn.
- Số chính phương chia cho 4 hoặc 3 không bao giờ có số dư là 2; số chính phương lẻ khi chia 8 luôn dư 1.
- Công thức để tính hiệu của hai số chính phương: a^2-b^2=(a+b)(a-b).
- Số ước nguyên dương của số chính phương là một số lẻ.
- Số chính phương chia hết cho số nguyên tố p thì chia hết cho p^2.
- Tất cả các số chính phương có thể viết thành dãy tổng của các số lẻ tăng dần từ 1: 1, 1 + 3, 1 + 3 + 5, 1 + 3 + 5 +7, 1 + 3 + 5 +7 +9 v.v...
S thỏa mãn các điều kiện trên nên S là số chính phương
22 tháng 12 2019
1+2+3+1= seven
còn nếu cộng tất là 28 ko là 7
nhớ t.i.c.k
cố mà trả lời nhé . A hihihihihihihihihi
3 - 1 = 2 + 0 = 4 - 2 = 5 - 3 = 6 - 4 = ...