Cho f(x) =ax^2+bx+c. Tính f(x+3) -3f(x+2) +3f(x+1) -f(x)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(f\left(x+3\right)-3f\left(x+2\right)+3f\left(x+1\right)\)
\(=a\left(x+3\right)^2+b\left(x+3\right)+c-3\left[a\left(x+2\right)^2+b\left(x+2\right)+c\right]+3\left[a\left(x+1\right)^2+b\left(x+1\right)+c\right]\)
\(=3a\left(x+1\right)^2+a\left(x+3\right)^2-3a\left(x+2\right)^2+bx+c\)
\(=ax^2+bx+c\)


Ta có:
f(x+3) = a(x+3)2+ b(x+3) +c=ax2+ (6a+b) x+ 9a+ 3b+c
f(x+2) = a(x+2)2+ b(x+2) +c=ax2+ (4a+b) x+ 4a+ 2b+c
f (x+1) = a(x+1)2+ b(x+1) +c=ax2+ (2a+b) x+ 2a+ 2b+c
Suy ra: (x+ 3) -3f( x+ 2) +3f( x+ 1)= ax2+ bx+ c
Chọn D.

Ta có: (x-2)5=(x-2)3.(x-2)2=(x3-6x2+12x-8)(x2-4x+4)=x5-6x4+12x3-8x2-4x4+24x3-48x2+32x+4x3-24x2+48x-32 = x5-10x4+40x3-32x2+80x-32
(x-1)4=(x-1)2(x-1)2 = (x2-2x+1)(x2-2x+1)=x4-2x3+x2-2x3+4x2-2x+x2-2x+1=x4-4x3+6x2-4x+1
Và: (x+1)2=x2+2x+1
=> P(x)= (x5-10x4+40x3-32x2+80x-32) + (x4-4x3+6x2-4x+1) + x3 +(x2+2x+1)+x+2
=> P(x)= x5-10x4+40x3-32x2+80x-32 + x4-4x3+6x2-4x+1 + x3 +x2+2x+1+x+2
=> P(x)= x5-9x4+37x3-25x2+79x-28
=> a=1; b=-9; c=37; d=-25; e=79; f=-28
=> a+3b+c+3d+e+3f = 1+3(-9)+37+3(-25)+79+3(-28) = 1-27+37-75+79-84=(1+37+79)-(27+75+84)=117-186
=> a+3b+c+3d+e+3f = - 69



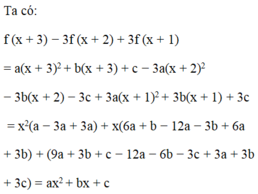
Lời giải:
Ta có: \(f(x)=ax^2+bx+c\)
\(\Rightarrow \left\{\begin{matrix} f(x+3)=a(x+3)^2+b(x+3)+c\\ f(x+2)=a(x+2)^2+b(x+2)+c\\ f(x+1)=a(x+1)^2+b(x+1)+c\\ f(x)=ax^2+bx+c\end{matrix}\right.\)
\(\Rightarrow f(x+3)-3f(x+2)+3f(x+1)-f(x)\)
\(=[f(x+3)-f(x)]-3[f(x+2)-f(x+1)]\)
Có:
\(f(x+3)-f(x)=a(x+3)^2+b(x+3)+c-[ax^2+bx+c]\)
\(=a[(x+3)^2-x^2]+b(x+3-x)\)
\(=3a(2x+3)+3b(1)\)
Và: \(f(x+2)-f(x+1)=a[(x+2)^2-(x+1)^2]+b[(x+2)-(x+1)]\)
\(=a(2x+3)+b\)
\(\Rightarrow 3[f(x+2)-f(x+1)]=3a(2x+3)+3b(2)\)
Từ (1)(2) suy ra:
\(f(x+3)-3f(x+2)+3f(x+1)-f(x)=3a(2x+3)+3b-[3a(2x+3)+3b]=0\)