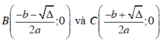Tìm Parabol (P): y=ax2+bx+c cắt trục hoành Ox tại 2 điểm có hoành độ lần lượt là -1 và 2, cắt trục tung Oy tại điểm có tung độ bằng -2.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 8 2021
a: Vì (d) đi qua hai điểm (0;5) và (-2;0) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}a\cdot0+b=5\\-2a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=5\\-2a=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=5\\a=\dfrac{5}{2}\end{matrix}\right.\)
CM
25 tháng 9 2017
Đồ thị hàm số y = a x + b cắt trục hoành tại điểm có hoành độ bằng 1 và cắt trục tung tại điểm có tung độ bằng 2
⇒ 1. a + b = 0 b = 2 ⇔ a = − 2 b = 2
Đáp án cần chọn là: D
7 tháng 12 2023
Sửa đề: cắt trục tung tại điểm có tung độ bằng -3
Thay x=0 và y=-3 vào (P), ta được:
\(a\cdot0^2+b\cdot0+c=-3\)
=>0+0+c=-3
=>c=-3
vậy: (P): \(y=ax^2+bx-3\)
Tọa độ đỉnh là I(-1;-4) nên ta có:
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=-1\\-\dfrac{b^2-4\cdot a\cdot\left(-3\right)}{4a}=-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=2a\\\dfrac{b^2+12a}{4a}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2a\\\left(2a\right)^2+12a=16a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=2a\\4a^2-4a=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2a\\4a\left(a-1\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=2a\\\left[{}\begin{matrix}a=0\left(loại\right)\\a-1=0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)
CM
30 tháng 3 2019
Đồ thị hàm số y = a x + b cắt trục hoành y = 0 ⇒ a x + b = 0 ⇔ x = − b a
ĐTHS y = a x + b cắt trục tung x = 0 ⇒ y = a . 0 + b ⇒ y = b
Vậy hàm số y = a x + b ( a ≠ 0 ) cắt trục hoành tại điểm có hoành độ bằng − b a và cắt trục tung tại điểm có tung độ bằng b
Đáp án cần chọn là: B
CM
20 tháng 11 2019
Điểm M có tung độ y = 1 nên hoành độ là
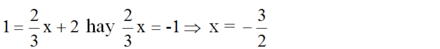
Điểm N có tung độ y = 1 nên hoành độ là
CM
5 tháng 12 2017
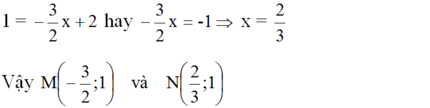
+ Giao điểm của parabol với trục tung:
Tại x = 0 thì y = a.02 + b.0 + c = c.
Vậy giao điểm của parabol với trục tung là A(0 ; c).
+ Giao điểm của parabol với trục hoành :
Tại y = 0 thì ax2 + bx + c = 0 (*).
Để parabol cắt trục hoành tại hai điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt ⇔ Δ = b2 – 4ac > 0.
Khi Δ > 0 thì phương trình (*) có hai nghiệm là
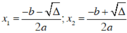
Tọa độ hai giao điểm là
