Bài 8: Cho đoạn thẳng AB, M thuộc đoạn thẳng AB. Vẽ về một phía của AB các tam giác đều AMC và BMD, AD giao MC tại E, BC giao MD tại F. Chứng minh:
a) Cho MA=a, MB=b. Tính ME, MF theo a,b
b) Tam giác MEF là tam giác gì?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 8 2019
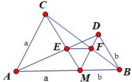
Vì các tam giác AMC và BMD đều nên B M D ^ = M A C ^ = 90 ° (vì hai góc ở vị trí đồng vị) => MD // AC
Vì MD // AC nên theo hệ quả định lý Talet cho hai tam giác DEM và AEC ta có M E E C = M D A C = b a
Suy ra
M E E C = b a ⇒ M E M E + E C = b b + a ⇒ M E a = b b + a ⇒ M E = a b b + a
Tương tự MF = b a a + b
Vậy M E = M F = a b b + a
Đáp án: B
Y
15 tháng 2 2019
1.
a) + ME // BD
\(\Rightarrow\dfrac{ME}{BD}=\dfrac{AM}{AB}=\dfrac{a}{a+b}\)
\(\Rightarrow\dfrac{ME}{b}=\dfrac{a}{a+b}\Rightarrow ME=\dfrac{ab}{a+b}\)
+ Tương tự : \(MF=\dfrac{ab}{a+b}\)
b) +ΔMEF có ME = MF, \(\widehat{EMF}=60^o\)
=> ΔMEF đều
2.
+ AB // CD \(\Rightarrow\dfrac{AE}{CF}=\dfrac{OE}{OF}\)
+ Tương tự : \(\dfrac{BE}{DF}=\dfrac{OE}{OF}\)
\(\Rightarrow\dfrac{BE}{DF}=\dfrac{AE}{CF}\) => DF = CF ( do AE = BE )
=> F là trung điểm của CD
CM
15 tháng 9 2017
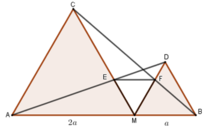
Đặt MB = a => MA = 2a
Vì các tam giác AMC và BMD đều nên B M D ^ = M A C ^ = 60 ° (hai góc ở vị trí đồng vị) => MD // AC
Vì MD // AC nên theo hệ quả định lý Talet cho hai tam giác DEM và AEC ta có
M E E C = M D A C = M B M A = 1 2
Suy ra:
M E E C = b a ⇒ M E M E + E C = 1 1 + 2 = 1 3 ⇒ M E 2 a = 1 3 ⇒ M E = 2 a 3
Tương tự MF = 2 a 3
Vậy M E = M F = 2 a 3
Đáp án: B
MS
8 tháng 1 2018
7)
a) ta có:
\(\widehat{AKE}=\widehat{BAD}\) (đồng vị và AD//KM)
\(\widehat{AEK}=\widehat{DAE}\) (so le trong và AD//KM)
\(\widehat{BAD}=\widehat{DAE}\) (AD là tia phân giác)
=> \(\widehat{AKE}=\widehat{AEK}\)
=> tam giác AKE cân tại A
=> AK=AE
b) Xét tam giác BKM ta có:
AD//KM(gt)
=> \(\dfrac{BK}{AK}=\dfrac{MB}{MD}\) (Đlý thales thuận)
Xét tam giác ADC ta có:
AD//EM(gt)
=> \(\dfrac{CE}{AE}=\dfrac{CM}{MD}\) (Đlý thales thuận)
Mà AE=AK(cmt)
CM=MB(M là trung điểm BC)
Nên \(\dfrac{CE}{AK}=\dfrac{MB}{MD}\)
Mà \(\dfrac{BK}{AK}=\dfrac{MB}{MD}\) (cmt)
Nên CE=AB
MS
9 tháng 1 2018
9) Xét tam giác ODF ta có:
DF//EB(tc hthang ABCD)
=> \(\dfrac{DF}{EB}=\dfrac{FO}{EO}\) (Hệ quả Thales)
Xét tam giác OCF ta có:
CF//EA(tc hthang ABCD)
=> \(\dfrac{FC}{AE}=\dfrac{FO}{EO}\) (Hệ quả Thales)
Mà \(\dfrac{DF}{EB}=\dfrac{FO}{EO}\) (cmt)
AE=EB(E là trung điểm AB)
Nên DF=FC
=> F là trung điểm DC
CM
9 tháng 10 2018
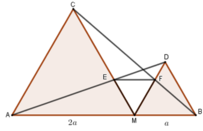
Ta có ME = MF => ΔEMF cân tại M
Ta có:
E M F ^ = 180 ° - C M A ^ - D M B ^ = 180 ° - 60 ° - 60 ° = 60 °
Từ đó MEF là tam giác cân có một góc bằng 60 ° nên nó là tam giác đều
Vậy EF = ME = MF = 2 a 3
Đáp án: A
CM
3 tháng 9 2017
Từ câu trước ta có ME = MF => ΔEMF cân tại M
Ta có A M C ^ + E M F ^ + D M B ^ = 180 ° mà C M A ^ = D M B ^ = 30 ° (tính chất tam giác đều)
Nên:
E M F ^ = 180 ° - M N A ^ - D M B ^ = 180 ° - 60 ° - 60 °
Từ đó MEF là tam giác cân có một góc bằng 60 ° nên nó là tam giác đều
Đáp án: A
a) Ta có:
\(\widehat{CMA}=\widehat{DBA}\left(=60^o\right)\)
Mà 2 góc nằm ở vị trí đồng vị
=> EM//BD
Xét tam giác ABD ta có:
EM//BD(cmt)
=> \(\dfrac{EM}{BD}=\dfrac{AM}{AB}\Rightarrow\dfrac{EM}{b}=\dfrac{a}{ab}\Rightarrow EM=1\)
Cmtt: \(\dfrac{FM}{AC}=\dfrac{BM}{AB}\Rightarrow\dfrac{FM}{b}=\dfrac{a}{ab}\Rightarrow FM=1\)
b) Ta có:
FM=EM(=1)
=> tam giác EMF cân tại M
Ta có:
\(\widehat{CMA}+\widehat{EMF}+\widehat{DMB}=180^o\)
\(60^o+\widehat{EMF}+60^o=180^o\)
\(\widehat{EMF}=60^o\)
Xét tam giác EMF cân tại M ta có:
\(\widehat{EMF}=60^o\) (cmt)
=> tam giác EMF đều