cho hình bình hành ABCD có AB=a , BC=b, BD=m ,AC=n . chứng minh rằng:
m2 +n2 =2 (a2+b2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
20 tháng 9 2017
Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD.
Xét ΔABC có BO là trung tuyến
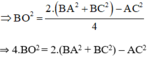
Mà O là trung điểm của BD nên BD = 2. BO ⇒ BD2 = 4. BO2
⇒ BD2 = 2.(AB2 + BC2) – AC2
⇒ BD2 + AC2 = 2.(AB2 + BC2)
⇒ m2 + n2 = 2.(a2 + b2) (ĐPCM).
AT
30 tháng 3 2017
Áp dụng định lí về đường trung tuyến:
OA2 = -
(1)
Thay OA = , AB = a, AD = BC = b và BD = m vào (1) ta có:
\(\left(\dfrac{n}{2}\right)^2=\dfrac{b^2+a^2}{2}-\dfrac{m^2}{4}\)
\(\Leftrightarrow\dfrac{n^2}{4}+\dfrac{m^2}{4}=\dfrac{a^2+b^2}{2}\)
\(\Leftrightarrow m^2+n^2=2\left(a^2+b^2\right)\)
21 tháng 1 2022
Gọi giao điểm của AC và BD là O
Ta có: \(OB^2=\dfrac{2\left(AB^2+BC^2\right)-AC^2}{4}\)
\(\Leftrightarrow\) \(4OB^2+AC^2=2\left(AB^2+BC^2\right)\)
\(\Leftrightarrow\) \(BD^2+AC^2=2\left(AB^2+BC^2\right)\) (Do \(4OB^2=\left(2OB\right)^2\) mà 2OB = BD)
\(\Leftrightarrow\) \(m^2+n^2=2\left(a^2+b^2\right)\) (đpcm)
Chúc bn học tốt!
LT
1
13 tháng 4 2016
Áp dụng định lí về đường trung tuyến:
OA2 = –
Thay OA = , AB = a
AD = BC = b và BD = m => dpcm
OL
3
TM
28 tháng 8 2021
- Gọi E là giao điểm của AC và BD
△ABE có trung tuyến BE
\(\Rightarrow BE^2=\dfrac{2\left(AB^2+BC^2\right)-AC^2}{4}\)
\(\Rightarrow4.BE^2=2\left(AB^2+BC^2\right)-AC^2\)
Mà O là trung điểm BD \(\Rightarrow BD=2.BE\Rightarrow BD^2=4.BE^2\)
\(\Rightarrow BD^2=2\left(AB^2+BC^2\right)-AC^2\)
\(\Rightarrow BD^2+AC^2=2\left(AB^2+BC^2\right)\)
Vậy: \(AC^2+BD^2=2\left(a^2+b^2\right)\left(đpcm\right)\)
(Hình như đây là Toán 10?)
AH
Akai Haruma
Giáo viên
28 tháng 8 2021
Lời giải:
Kẻ đường cao $BH, DT$ của hình bình hành
Dễ chứng minh $\triangle ADT =\triangle BCH$ (ch-gn)
$\Rightarrow DT=CH; AT=BH$
Áp dụng định lý Pitago:
$AC^2+BD^2=AT^2+TC^2+BH^2+DH^2$
$=(AT^2+BH^2)+TC^2+DH^2)$
$=2AT^2+(DC-DT)^2+(DC+CH)^2$
$=2(AD^2-DT^2)+(DC-DT)^2+(DC-DT)^2$
$=2(b^2-DT^2)+(a-DT)^2+(a+DT)^2$
$=2(b^2+a^2)$
Ta có đpcm.
4 tháng 10 2015
(Tự vẽ hình nhen)
a,Ta có ABCD là hbh => gADC=gABC(1)
BM là phân giác gABC(gt)=>gABM=1/2gABC(2)
DN là phân giác gADC(gt)=>gMDN=1/2gADC(3)
Từ(1),(2) và (3)=> gNDM=gNBM
Mặt khác NB//DM(t/c hbh)=> BMDN là hbh
b,Gọi O là giao điểm của AC và BD(4)
=>O là trung điểm của BD(t/c hbh)
Ta lại có BMDN là hbh(câu a)=>O cũng là trung điểm của MN(5)
Từ (4) và (5)=>AC,BD,MN đồng quy tại O
Gọi O là giao điểm của AC va BD
\(AO^2=\dfrac{2\left(a^2+b^2\right)-m^2}{4}\)
⇒\(\dfrac{n^2}{4}=\dfrac{2\left(a^2+b^2\right)-m^2}{4}\)
⇒\(n^2=2\left(a^2+b^2\right)-m^2\)
⇒⇒\(n^2+m^2=2\left(n^2+m^2\right)\)