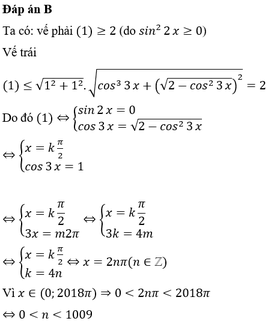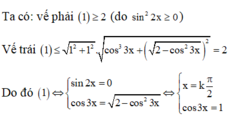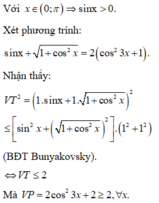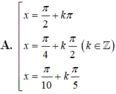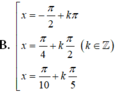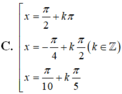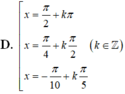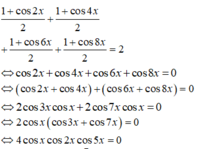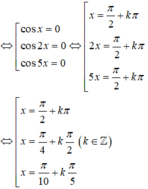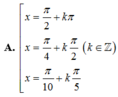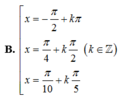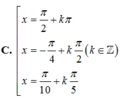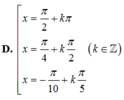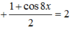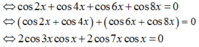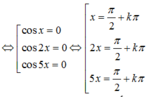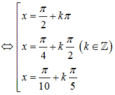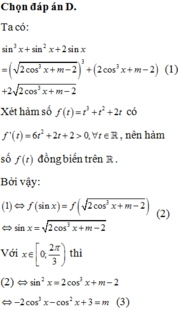Cos3x + √2-cos23x = 2(1+sin22x)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1-sin^23x-5sin3x+5=0\)
\(\Leftrightarrow-sin^23x-5sin3x+6=0\)
\(\Rightarrow\left[{}\begin{matrix}sin3x=1\\sin3x=-6< -1\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow3x=\dfrac{\pi}{2}+k2\pi\)
\(\Rightarrow x=\dfrac{\pi}{6}+\dfrac{k2\pi}{3}\)

Phương trình đã cho tương đương với:
1 + cos 2 x 2 + 1 + cos 4 x 2 + 1 + cos 6 x 2 + 1 + cos 8 x 2 = 2 ⇔ cos 2 x + cos 4 x + cos 6 x + cos 8 x = 0 ⇔ cos 2 x + cos 4 x + cos 6 x + cos 8 x = 0 ⇔ 2 cos 3 x cos x + 2 cos 7 x cos x = 0 ⇔ 2 cos x cos 3 x + cos 7 x = 0 ⇔ 4 cos x cos 2 x cos 5 x = 0 ⇔ cos x = 0 cos 2 x = 0 cos 5 x = 0 ⇔ x = π 2 + k π x = π 4 + k π 2 x = π 10 + k π 5
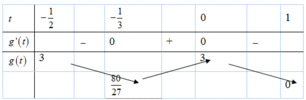
Đáp án A

\(\Leftrightarrow sin^25x+sin^23x=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}sin3x=0\\sin5x=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{k\pi}{3}\\x=\dfrac{k\pi}{5}\end{matrix}\right.\)
\(\Leftrightarrow x=k\pi\)

Chọn C.
Áp dụng , với u = 2 + sin22x.
y' = 3(2 + sin22x)2(2 + sin22x)’ = 3(2 + sin22x)2(sin22x)’.
Tính (sin22x)’, áp dụng với u = sin2x
(sin22x)’ = 2.sin2x(sin2x)’ = 2.sin2x.cos2x(2x)’ = 2sin4x.
⇒ y' = 6sin4x(2 + sin22x)2.