Tìm x thuộc N để :2017x2 + 2017x + 13 chia hết x+1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 1 2017
Đáp án D.
Phương pháp:
Sử dụng phương pháp hàm số giải bất phương trình (1), suy ra điều kiện của nghiệm x.
Bất phương trình (2), cô lập m, đưa về dạng m ≥ f(x) trên [a;b] có nghiệm 
Cách giải: ĐK: x ≥ –1
Xét hàm số 
có 
=> Hàm số đồng biến trên R
Để hệ phương trình có nghiệm thì phương trình (2) có nghiệm 
Với 
Để phương trình có nghiệm 
(sử dụng MTCT để tìm GTNN)
SN
0
NY
0
B
23 tháng 11 2019
(1) Tìm x thuộc N biết 18 chia hết cho x khi x-2
Để 18 chia hết cho x khi x-2
=> 18 chia hết cho x-2
=> x-2 thuộc Ư(18) = {1;2;3;6;9;18}
Ta có bảng:
| x-2 | 1 | 2 | 3 | 6 | 9 | 18 |
| x | 3 | 4 | 5 | 8 | 11 | 20 |
Vậy x thuộc {3;4;5;8;11;20}
(2) Tìm x thuộc N biết x-1 chia hết cho 13
Để x-1 chia hết cho 13 => x-1 thuộc B(13) = {0;13;26;49;...}
=> x thuộc {1;14;27;30;...}
(3) Tìm x thuộc N biết x+10 chia hết cho x-2
Để x+10 chia hết cho x-2
=> (x-2)+12 chia hết cho x-2
Mà x-2 chia hết cho x-2
=> x-2 thuộc Ư(12) = {1;2;3;4;6;12}
Ta có bảng:
| x-2 | 1 | 2 | 3 | 4 | 6 | 12 |
| x | 3 | 4 | 5 | 6 | 8 | 14 |
Vậy x thuộc {3;4;5;6;8;14}
NT
1
1 tháng 2 2017
(x+13) chia hết cho (x+2)
=> (x+1)+12 chia hết cho (x+2)
=> 12 chia hết cho x+2
=> x+2 \(\in\)Ư(12)
mà Ư(12)={1;2;3;4;6;12}
=>x+2=1=>x=-1 (loại)
=>x+2=2=> x=0 (thỏa mãn)
các th sau tự giải
(x+5) chia hết cho (x+1)
=> (x+1)+4 chia hết cho (x+1)
=> 4 chia hết cho (x+1)
=> (x+1)\(\in\)Ư(4)
mà Ư(4)={1;2;4}
bn làm từng trường hợp và kết luận nhé! nhơ là nếu x là số âm thì loại
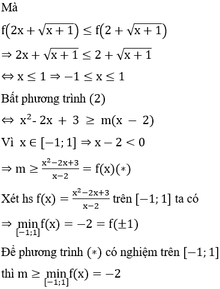
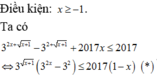
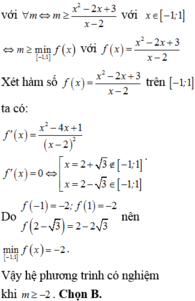
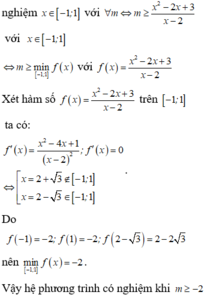
\(2017x^2+2017x+13⋮x+1\\ \Rightarrow2017x\left(x+1\right)+13⋮x+1\\ \Rightarrow13⋮x+1\\ \Rightarrow x+1\in U\left(13\right)=\left\{1;13\right\}\\ \Rightarrow x\in\left\{0;12\right\}\)