a) Chứng minh rằng tứ giác 𝐵𝐻𝐶𝐷 là hình bình hành.
b) Biết 𝐵𝐴𝐶 ̂ = 60^𝑜, tính số đo góc 𝐵𝐻𝐶 ̂.
c) Chứng minh rằng 𝐻, 𝐸, 𝐷 thẳng hàng.
d) Chứng minh rằng 𝐴𝐻 = 2𝐹𝐸 và 𝐹𝐸 ⊥ 𝐵𝐶.
e) Chứng minh rằng 𝐴𝐻 = 2𝐼𝐽 và 𝐻, 𝐺, 𝐹 thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác BHCD có
CH//BD
BH//CD
Do đó: BHCD là hình bình hành

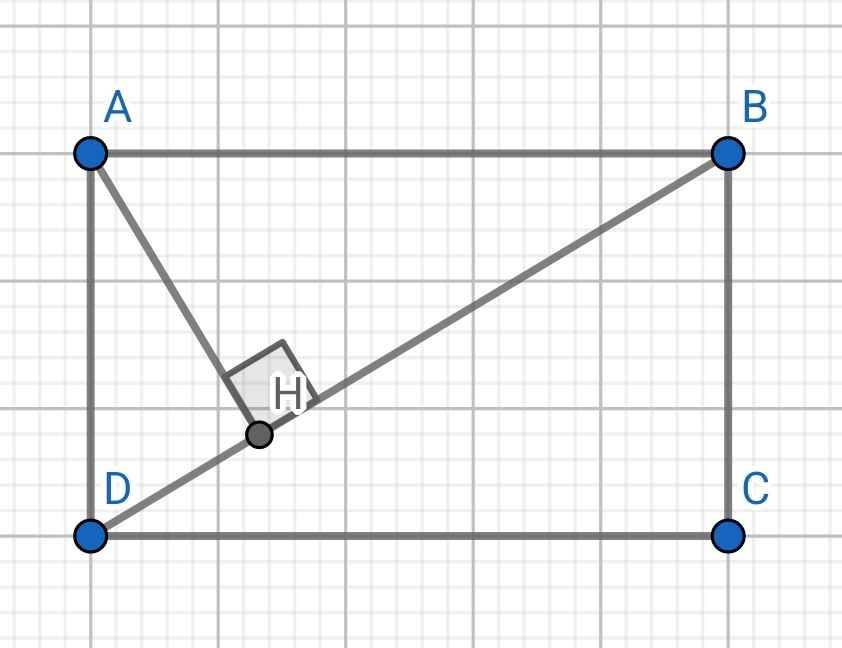
a) Xét hai tam giác vuông: ∆AHD và ∆BAD có:
∠D chung
⇒ ∆AHD ∽ ∆BAD (g-g)
b) *) Tính BD:
∆ABD vuông tại A (do ABCD là hình chữ nhật)
⇒ BD² = AB² + AD² (Pytago)
= 8² + 6²
= 100
⇒ BD = 10 (cm)
*) Tính AH:
Ta có: 1/2 . AH . BD = 1/2 . AB . AD (cùng bằng diện tích ∆ABD)
⇒ AH . BD = AB . AD
⇒ AH = (AB . AD) / BD
= 8.6/10
= 4,8 (cm)
c) Do ∆AHD ∽ ∆BAD (cmt)
⇒ AD/BD = HD/AD
⇒ AD.AD = BD.HD
⇒ AD² = BD.HD
Mà BC = AD (hai cạnh đối của hình chữ nhật)
⇒ BC² = BD.HD
a: Xet ΔAHD vuông tại H và ΔBAD vuông tại A có
góc ADH chung
=>ΔAHD đồng dạng với ΔBAD
b: \(BD=\sqrt{8^2+6^2}=10\left(cm\right)\)
AH=8*6/10=4,8cm
c: ΔABD vuông tại A có AH vuông góc BD
nên AD^2=DH*DB=BC^2

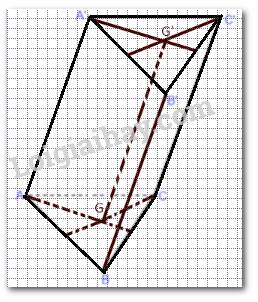
a) Ta có ABC.A'B'C' là hình lăng trụ nên \(\Delta ABC = \Delta A'B'C'\) suy ra AG = A'G'.
Lại có (ABC) // (A'B'C'), giao tuyến của mp(AGG'A') với (ABC) và (A'B'C') lần lượt là AG, A'G' suy ra AG // A'G'.
Như vậy , tứ giác AGG'A' có AG = A'G', AG // A'G' là hình bình hành.
b) AGG'A' là hình bình hành suy ta AA' // GG'.
Lại có AA' // CC' (do ABC.A'B'C' là hình lăng trụ).
Mặt phẳng (AGC) // (A'G'C') suy ra AGC.A'G'C' là hình lăng trụ.

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Xét ΔADH có \(\widehat{DAH}=\widehat{DHA}\)
nên ΔADH cân tại D
c: Xét ΔABC có
H là trung điểm của BC
HD//AC
DO đó: D là trung điểm của AB
Xét ΔABC có
CD là đường trung tuyến
AH là đường trung tuyến
CD cắt AH tại G
Do đó: G là trọng tâm
=>B,G,E thẳng hàng

a: Xét tứ giác AMCN có
AM//CN
AN//CM
Do đó: AMCN là hình bình hành

a: Xét tứ giác AMCN có
AM//CN
AN//CM
Do đó: AMCN là hình bình hành
a: Xét tứ giác BHCD có
BH//CD
CH//BD
Do đó: BHCD là hình bình hành