Tìm x, y trên hình vẽ bên:
AH=6, BH =3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(BC=CH+HB=24\left(cm\right)\)
Áp dụng HTL: \(\left\{{}\begin{matrix}AB=\sqrt{BC\cdot BH}=12\left(cm\right)\\AC=\sqrt{BC\cdot CH}=12\sqrt{3}\left(cm\right)\end{matrix}\right.\)

Bài 3:
a: Xét ΔHAB có
M là trung điểm của HA
N là trung điểm của HB
Do đó: MN là đường trung bình
=>MN//AB và MN=AB/2
=>MN//KC và MN=KC
=>NCKM là hình bình hành
b; Xét ΔBMC có
BH là đường cao
MN là đường cao
BH cắt MN tại N
DO đó:N là trực tâm
=>CN vuông góc với BM
=>BM vuông góc với MK
hay góc BMK=90 độ

Đề có cho thêm dữ kiện gì không bạn? Vì nếu hình như thế này thì không tìm được x,y

Đáp án C.
Quan sát đồ thị hàm số, ta thấy có hai điểm cực đại thuộc đoạn [-2; 3]

Đáp án B
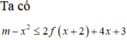
![]()
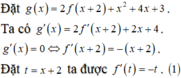
(1) là phương trình hoành độ giao điểm của đồ thị f'(t) và đường thẳng d : y = -t (hình vẽ)
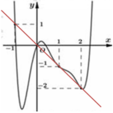
Dựa vào đồ thị của f'(t) và đường thẳng y =-t ta có




Mìk tính y :
Ta có: TDE + DET + DTE = 180o
\(x=\dfrac{AH^2}{HB}=\dfrac{6^2}{9}=4\)
\(y=\sqrt{12^2+4^2}=4\sqrt{10}\)
đường cao AH đúng k bạn