Cho ΔABC, trên tia đối của tia AB lấy Điểm D sao cho AD=AB, trên tia đối của tia AC lấy điểm E sao cho AE=AC.
a. Chứng minh: Δ ABC = Δ ADE,suy ra BC//DE
b. Vẽ AI,AK theo thứ tự là các tia phân giác của góc BAC và góc DAE (I ∈ BC; K ∈ DE).Chứng minh:AI=AK
c.Chứng minh ba điểm I,A,K thẳng hàng.
Hellp me ~~~ Mai nộp rồi giúp nha huhu thanks ai giúp nha...
Đọc tiếp
Cho ΔABC, trên tia đối của tia AB lấy Điểm D sao cho AD=AB, trên tia đối của tia AC lấy điểm E sao cho AE=AC.
a. Chứng minh: Δ ABC = Δ ADE,suy ra BC//DE
b. Vẽ AI,AK theo thứ tự là các tia phân giác của góc BAC và góc DAE (I ∈ BC; K ∈ DE).Chứng minh:AI=AK
c.Chứng minh ba điểm I,A,K thẳng hàng.
Hellp me ~~~ Mai nộp rồi giúp nha huhu thanks ai giúp nha
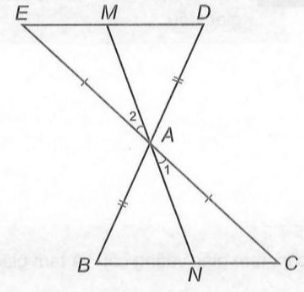
a)△ABC,△ADE có :
c : AB=AD(gt)
g : \(\widehat{BAC}=\widehat{DAE}\)
c : AC=AE(gt)
\(\Rightarrow\)△ABC=△ADE(c.g.c)
\(\Rightarrow\)\(\widehat{EDA}=\widehat{ACB}(2 g.t.ư)\)(1)
Mà 2 góc ở vị trí so le trong
\(\Rightarrow\)BC//DE
b)Ta có : AI là p/giác \(\widehat{BAC}\)\(\Rightarrow\)\(\widehat{A_{1}}=\widehat{A_{2}}\)(2)
AK là p/giác \(\widehat{DAE}\)\(\Rightarrow\)\(\widehat{A_{3}}=\widehat{A_{4}}\)(3)
Từ(1)(2)(3)\(\Rightarrow\)\(\widehat{A_{1}}=\widehat{A_{2}}=\widehat{A_{3}}=\widehat{A_{4}}\)(4)
△AEK=ΔACI(c.g.c)(cái này bạn tự ghi điều kiện ra nha, mk làm biếng ><)
\(\Rightarrow\)\(\left\{{}\begin{matrix}AI=AK\left(2c.t.\text{ư}\right)\\\end{matrix}\right.\)
Ta có : \(\widehat{A_{2}} +\widehat{IAE}=180^{0}\)(5)
Từ (5)(4)\(\Rightarrow\)\(\widehat{A_{3}}+\widehat{IAE}=180^{0}\)
\(\Rightarrow\)\(\widehat{IAK}=180^{0}\)
\(\Rightarrow\)I,A,K thẳng hàng.
XONG RÙI ĐÓ. CHÚC HỌC TỐT!!!!
Ơ...What the hell!? Rõ ràng lúc mk ghi thì bình thường mà sao ấn "Gửi câu trả lời" thì nó lại ra cái nùi giẻ thế này. Ôi giời ơi. Nãy giờ tốn công ngồi viết. Huhuhuhuhu...
HẬN!!!!!!!