giúp mình nha : x3=y5 và x+y=49
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^5+y^5=\left(x^2+y^2\right)\left(x^3+y^3\right)-x^2y^3-x^3y^2\)
\(=\left(x^2+y^2\right)\left(x^3+y^3\right)-\left(xy\right)^2\left(x+y\right)\)
\(=10.26-\left(-3\right)^2.2=...\)
(x+y)5=32
⇔ x5+5x4y+10x3y2+10x2y3+5xy4+y5 = 32
⇔ x5+y5 = 32-5xy(x3+y3)-10x2y2(x+y)
= 32-5.(-3).26-10.(-3)2.2
= 242

Tính: A=x^3+y^3
A=x^3+y^3
A=(x+y)(x^2-xy+y^2)
A=3 . [(x^2+y^2)-xy]
A=3 . (5-xy)
A=15-3xy
2.Cho x-y=5 và x^2+y^2=15
Tính B= x^3-y^3
B=x^3-y^3
B=(x-y)(x^2+xy+y^2)
B=5 . [(x^2+y^2)+xy]
B=5 . (15+xy)
B=75+5xy
Ta có: \(x+y=3\)
\(\Rightarrow\left(x+y\right)^2=9\)
\(\Rightarrow x^2+y^2+2xy=9\)
\(\Rightarrow2xy+5=9\Rightarrow2xy=4\Rightarrow xy=2\)
a) \(x^3+y^3=\left(x+y\right)\left(x^2-xy+y^2\right)=3\left(5-2\right)=9\)

a: \(f\left(x\right)+g\left(x\right)=2x^3-2x^2+4x\)
b: \(f\left(x\right)-g\left(x\right)=-2x^2+2x+2\)
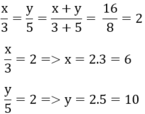
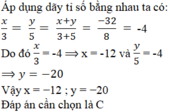
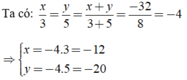
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x+y}{3+5}=\dfrac{49}{8}\)
Do đó: \(\left\{{}\begin{matrix}x=\dfrac{147}{8}\\y=\dfrac{245}{8}\end{matrix}\right.\)