1 . Cho biểu thức 222+242+262+...+422=11704. Tính S=112+122+132+142+...+212
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 8 2019
Ta có: 102+112+122 = 100 + 121 + 144 = 365
132+142 = 169 + 196 = 365
Vậy 102+112+122 = 132+142
NB
1
BV
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
30 tháng 10 2023
(102 + 112 + 122) : (132 + 142)
= (100 + 121 + 144) :( 169 + 196)
= 365: 365
= 1
PT
1
CM
3 tháng 10 2018
1 2 2 < 1 1.2 ; 1 3 2 < 1 2.3 ; 1 4 2 < 1 3.4 ; ... ; 1 10 2 < 1 9.10
⇒ 1 2 2 + 1 3 2 + 1 4 2 + 1 10 2 < 1 1.2 + 1 2.3 + 1 3.4 + ... + 1 9.10 < 1.
PT
1
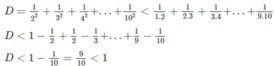
Ta có: \(S=11^2+12^2+13^2+14^2+...+21^2\)
\(=\left(11.2\right)^2+\left(12.2\right)^2+\left(13.2\right)^2+\left(14.2\right)^2+...+\left(21.2\right)^2\)
\(=22^2+24^2+26^2+28^2+...+42^2\)
\(=11704\)
Vậy S=11704
sai rồi bạn ơi