Tìm giá trị nhỏ nhất của :
Q = a2 + 4b2-10a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A.
$a^2+4b^2+9c^2=2ab+6bc+3ac$
$\Leftrightarrow a^2+4b^2+9c^2-2ab-6bc-3ac=0$
$\Leftrightarrow 2a^2+8b^2+18c^2-4ab-12bc-6ac=0$
$\Leftrightarrow (a^2+4b^2-4ab)+(a^2+9c^2-6ac)+(4b^2+9c^2-12bc)=0$
$\Leftrightarrow (a-2b)^2+(a-3c)^2+(2b-3c)^2=0$
$\Rightarrow a-2b=a-3c=2b-3c=0$
$\Rightarrow A=(0+1)^{2022}+(0-1)^{2023}+(0+1)^{2024}=1+(-1)+1=1$
B.
$x^2+2xy+6x+6y+2y^2+8=0$
$\Leftrightarrow (x^2+2xy+y^2)+y^2+6x+6y+8=0$
$\Leftrightarrow (x+y)^2+6(x+y)+9+y^2-1=0$
$\Leftrightarrow (x+y+3)^2=1-y^2\leq 1$ (do $y^2\geq 0$ với mọi $y$)
$\Rightarrow -1\leq x+y+3\leq 1$
$\Rightarrow -4\leq x+y\leq -2$
$\Rightarrow 2020\leq x+y+2024\leq 2022$
$\Rightarrow A_{\min}=2020; A_{\max}=2022$

a) Ta có: \(M=-x^2-4x+20\)
\(=-\left(x^2+4x-20\right)\)
\(=-\left(x^2+4x+4-24\right)\)
\(=-\left(x+2\right)^2+24\le24\forall x\)
Dấu '=' xảy ra khi x=-2

Điều kiện x ≠ 2 và x ≠ 0
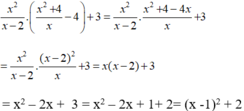
Vì x - 1 2 ≥ 0 nên x - 1 2 + 2 ≥ 2 với mọi giá trị của x.
Khi đó giá trị nhỏ nhất của biểu thức bằng 2 khi x = 1.
Vậy biểu thức đã cho có giá trị nhỏ nhất bằng 2 tại x = 1.


Lời giải:
$P=(4a^2+4ab+b^2)-12a-12b+3b^2+12$
$=(2a+b)^2-6(2a+b)+3b^2-6b+12$
$=(2a+b)^2-6(2a+b)+9+3(b^2-2b+1)$
$=(2a+b-3)^2+3(b-1)^2\geq 0+3.0=0$
Vậy $P_{\min}=0$
Giá trị này đạt tại $2a+b-3=b-1=0$
$\Rightarrow b=1; a=1$
Lời giải:
$P=(4a^2+4ab+b^2)-12a-12b+3b^2+12$
$=(2a+b)^2-6(2a+b)+3b^2-6b+12$
$=(2a+b)^2-6(2a+b)+9+3(b^2-2b+1)$
$=(2a+b-3)^2+3(b-1)^2\geq 0+3.0=0$
Vậy $P_{\min}=0$
Giá trị này đạt tại $2a+b-3=b-1=0$
$\Rightarrow b=1; a=1$

C=2a2+b2-2ab+10a+42
=a2-2ab+b2+a2+10a+25+17
=(a-b)2+(a+5)2+17
=>MIN(C)=17 <=>a-b=0 và a+5=0
<=>a=b=-5
vậy ..................

Q=a^2+4b^2-10a
Q=a^2-5a-5a+25+4b^2-25
Q=a(a-5)-5(a-5)+4b^2-25
Q=(a-5)^2+4b^2-25 >=-25
Dấu "=" xảy ra khi a-5=0;b=0
<=> a=5;b=0
Vậy Min Q=-25 khi a=5;b=0
a2+4b2-10a
=a2-10a+4b2
=a2-10a+25+4b2-25
=(a-5)2+4b2-25
Vì (a-5)2>=0 với mọi a.Dấu bằng xảy ra khi a-5=0
<=> a =5
Lại có 4b2>=0 với mọi b.Dấu bằng xảy ra khi 4b2=0
<=> b2 =0
<=> b =0
=>(a-5)2+4b2-25>=-25 với mọi a;b.Dấu bắng xảy ra khi a=5;b=0
Vậy giá trị nhỏ nhất của Q là -25 tại a=5;b=0

2:
a: =>a^2+2ab+b^2-2a^2-2b^2<=0
=>-(a^2-2ab+b^2)<=0
=>(a-b)^2>=0(luôn đúng)
b; =>a^2+b^2+c^2+2ab+2ac+2bc-3a^2-3b^2-3c^2<=0
=>-(2a^2+2b^2+2c^2-2ab-2ac-2bc)<=0
=>(a-b)^2+(b-c)^2+(a-c)^2>=0(luôn đúng)
a2+4b2-10a=(a2-10a+25)+4b2-25
=(a-52)+4b2 -25>25
bn ơi bn làm z thì ngoài ngoặc còn 4ab2-25 nên phải là > 4ab2-25 chứ bn