Tính giá trị biểu thức: \(\left(1-\dfrac{1}{2^2}\right)\left(1-\dfrac{1}{3^2}\right)\left(1-\dfrac{1}{4^2}\right)...\left(1-\dfrac{1}{2017^2}\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 1 2022
e: \(=\left(\dfrac{18}{37}+\dfrac{19}{37}\right)+\left(\dfrac{8}{24}+\dfrac{2}{3}\right)-\dfrac{47}{24}=2-\dfrac{47}{24}=\dfrac{1}{24}\)
f: \(=-8\cdot\dfrac{1}{2}:\left(\dfrac{9}{4}-\dfrac{7}{6}\right)\)
\(=-4:\dfrac{13}{12}=\dfrac{-48}{13}\)
g: \(=\dfrac{4}{25}+\dfrac{11}{2}\cdot\dfrac{5}{2}-\dfrac{8}{4}=\dfrac{4}{25}+\dfrac{55}{4}-2=\dfrac{1191}{100}\)
Y
21 tháng 6 2023
\(a,\left(7+3\dfrac{1}{4}-\dfrac{3}{5}\right)+\left(0,4-5\right)-\left(4\dfrac{1}{4}-1\right)\)
\(=\left(7+\dfrac{13}{4}-\dfrac{3}{5}\right)-\dfrac{23}{5}-\left(\dfrac{17}{4}-1\right)\)
\(=7+\dfrac{13}{4}-\dfrac{3}{5}-\dfrac{23}{5}-\dfrac{17}{4}+1\)
\(=\left(7+1\right)+\left(\dfrac{13}{4}-\dfrac{17}{4}\right)-\left(\dfrac{3}{5}+\dfrac{23}{5}\right)\)
\(=8-\dfrac{4}{4}-\dfrac{26}{5}\)
\(=7-\dfrac{26}{5}\)
\(=\dfrac{9}{5}\)
\(b,\dfrac{2}{3}-\left[\left(-\dfrac{7}{4}\right)-\left(\dfrac{1}{2}+\dfrac{3}{8}\right)\right]\)
\(=\dfrac{2}{3}-\left(-\dfrac{7}{4}-\dfrac{1}{2}-\dfrac{3}{8}\right)\)
\(=\dfrac{2}{3}-\left(-\dfrac{14}{8}-\dfrac{4}{8}-\dfrac{3}{8}\right)\)
\(=\dfrac{2}{3}-\left(-\dfrac{21}{8}\right)\)
\(=\dfrac{2}{3}+\dfrac{21}{8}\)
\(=\dfrac{79}{24}\)
\(c,\left(9-\dfrac{1}{2}-\dfrac{3}{4}\right):\left(7-\dfrac{1}{4}-\dfrac{5}{8}\right)\)
\(=\left(\dfrac{36}{4}-\dfrac{2}{4}-\dfrac{3}{4}\right):\left(\dfrac{56}{8}-\dfrac{2}{8}-\dfrac{5}{8}\right)\)
\(=\dfrac{31}{4}:\dfrac{49}{8}\)
\(=\dfrac{62}{49}\)
\(d,3-\dfrac{1-\dfrac{1}{7}}{1+\dfrac{1}{7}}=3-\dfrac{\dfrac{7}{7}-\dfrac{1}{7}}{\dfrac{7}{7}+\dfrac{1}{7}}=3-\left(\dfrac{6}{7}:\dfrac{8}{7}\right)=3-\dfrac{3}{4}=\dfrac{9}{4}\)
BA
21 tháng 11 2023
a) = (\(-\dfrac{141}{20}\)- \(\dfrac{1}{4}\)) : (-5) + \(\dfrac{1}{15}\) - \(\dfrac{1}{15}\)
= \(-\dfrac{73}{10}\) : - 5
= \(\dfrac{73}{50}\)
b) = \(\left(\dfrac{3}{25}-\dfrac{28}{25}\right)\). \(\dfrac{7}{3}\) : \(\left(\dfrac{7}{2}-\dfrac{11}{3}.14\right)\)
= \(-\dfrac{7}{3}\) . \(-\dfrac{6}{287}\)
= \(\dfrac{2}{41}\)
VV
22 tháng 7 2021
B = \(\left(-1\dfrac{1}{6}\right)\) : \(\left(\dfrac{-10}{3}+\dfrac{9}{4}\right)\) - \(\left(-\dfrac{3}{8}\right)\) : \(\left(8-\dfrac{51}{8}\right)\)
B = \(\dfrac{-7}{6}\) : \(\dfrac{-13}{12}\) - \(\left(-\dfrac{3}{8}\right)\) : \(\dfrac{13}{8}\)
B = \(\dfrac{14}{13}\) - \(\dfrac{-3}{13}\)
B = \(\dfrac{17}{13}\)
7 tháng 1
a: \(A=3^{\dfrac{2}{5}}\cdot3^{\dfrac{1}{5}}\cdot3^{\dfrac{1}{5}}=3^{\dfrac{2}{5}+\dfrac{1}{5}+\dfrac{1}{5}}=3^{\dfrac{4}{5}}\)
b: \(B=\left(-27\right)^{\dfrac{1}{3}}=\left[\left(-3\right)^3\right]^{\dfrac{1}{3}}=\left(-3\right)^{\dfrac{1}{3}\cdot3}=\left(-3\right)^1=-3\)
c: \(C=\sqrt[3]{-64}\cdot\left(\dfrac{1}{2}\right)^3\)
\(=\sqrt[3]{\left(-4\right)^3}\cdot\dfrac{1}{2^3}=-4\cdot\dfrac{1}{8}=-\dfrac{4}{8}=-\dfrac{1}{2}\)
d: \(D=\left(-27\right)^{\dfrac{1}{3}}\cdot\left(\dfrac{1}{3}\right)^4\)
\(=\left[\left(-3\right)^3\right]^{\dfrac{1}{3}}\cdot\dfrac{1}{3^4}\)
\(=\left(-3\right)^{3\cdot\dfrac{1}{3}}\cdot\dfrac{1}{81}=\dfrac{-3}{81}=\dfrac{-1}{27}\)
e: \(E=\left(\sqrt{3}+1\right)^{106}\cdot\left(\sqrt{3}-1\right)^{106}\)
\(=\left[\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)\right]^{106}\)
\(=\left(3-1\right)^{106}=2^{106}\)
f: \(F=360^{\sqrt{5}+1}\cdot20^{3-\sqrt{5}}\cdot18^{3-\sqrt{5}}\)
\(=360^{\sqrt{5}+1}\cdot\left(20\cdot18\right)^{3-\sqrt{5}}\)
\(=360^{\sqrt{5}+1}\cdot360^{3-\sqrt{5}}=360^{\sqrt{5}+1+3-\sqrt{5}}=360^4\)
g: \(G=2023^{3+2\sqrt{2}}\cdot2023^{2\sqrt{2}-3}\)
\(=2023^{3+2\sqrt{2}+2\sqrt{2}-3}\)
\(=2023^{4\sqrt{2}}\)
25 tháng 5 2022
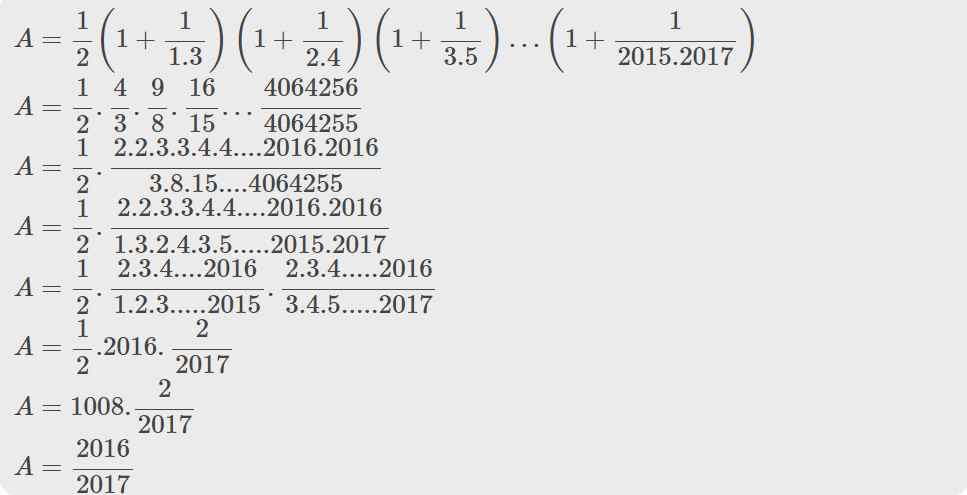
\(A=\dfrac{1}{2}.\left(1+\dfrac{1}{1.3}\right)\left(1+\dfrac{1}{2.4}\right)\left(1+\dfrac{1}{3.5}\right)....\left(\dfrac{1}{2015.2017}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1}.\dfrac{2}{3}\right).\left(\dfrac{3}{2}.\dfrac{3}{4}\right).\left(\dfrac{4}{3}.\dfrac{4}{5}\right)....\left(\dfrac{2016}{2015}.\dfrac{2016}{2017}\right)\)
\(=\dfrac{1}{2}.\left(\dfrac{2}{1}.\dfrac{2}{3}\right).\left(\dfrac{3}{2}.\dfrac{3}{4}\right).\left(\dfrac{4}{3}.\dfrac{4}{5}\right).....\left(\dfrac{2016}{2015}.\dfrac{2016}{2017}\right)\)
\(=\dfrac{2016}{2017}\)
12 tháng 7 2023
\(=\dfrac{1}{2}\cdot\dfrac{2^2-1+1}{\left(2-1\right)\left(2+1\right)}\cdot\dfrac{3^2-1+1}{\left(3-1\right)\left(3+1\right)}\cdot...\cdot\dfrac{2016^2-1+1}{\left(2016-1\right)\left(2016+1\right)}\)
\(=\dfrac{1}{2}\cdot\dfrac{2}{1}\cdot\dfrac{3}{2}\cdot...\cdot\dfrac{2016}{2015}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot...\cdot\dfrac{2016}{2017}\)
\(=\dfrac{1}{2}\cdot2016\cdot\dfrac{2}{2017}=\dfrac{2016}{2017}\)
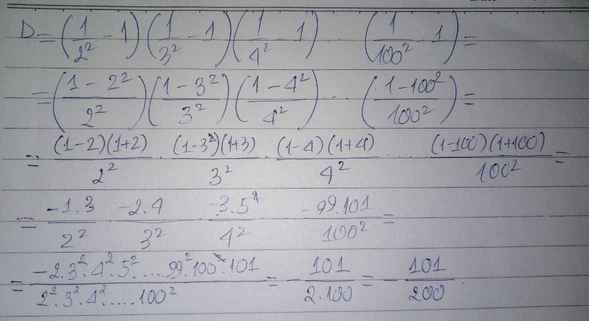
quy đồng lên ta đc \(\dfrac{2^2-1}{2^2}......\dfrac{2017^2-1}{2017^2}\)
khai triển hằng đẳng thức \(a^2-b^2=\left(a-b\right)\left(a+b\right)\)ta đc\(\dfrac{1.3}{2^2}.\dfrac{2.4}{3^2}.....\dfrac{2016.2018}{2017}\)
=\(\dfrac{1.2.3^2.4^2.....2016^2.2017.2018}{2^2.......2017^2}=\dfrac{1.2018}{2.2017}=\dfrac{1009}{2017}\)