tìm các giá trị của m để hai phương trình sau có ít nhất một nghiệm chung:
x2+2x+m=0 và x2+mx+2=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 3 2019
Gọi x0 là nghiệm chung của hai phương trình
thì x0 phải thỏa mãn hai phương trình trên.
Thay x = x0 vào hai phương trình trên ta được
x 0 2 + m x 0 + 2 = 0 x 0 2 + 2 x 0 + m = 0
⇒ (m – 2)x0 + 2 – m = 0 ⇔ (m – 2)(x0 – 1) = 0
Nếu m = 2 thì 0 = 0 (luôn đúng) hay hai phương trình trùng nhau.
Lúc này phương trình x2 + 2x + 2 = 0 ⇔ (x + 1)2 = −1
vô nghiệm nên cả hai phương trình đều vô nghiệm
Vậy m = 2 không thỏa mãn.
Nếu m ≠ 2 thì x0 = 1
Thay x0 = 1 vào phương trình x02 + mx0 + 2 = 0
ta được 1 + m + 2 = 0 ⇔ m = −3
Vậy m = −3 thì hai phương trình có nghiệm chung
Đáp án cần chọn là: B
27 tháng 4 2020
2.giải phương trình trên , ta được :
\(x_1=\frac{-m+\sqrt{m^2+4}}{2};x_2=\frac{-m-\sqrt{m^2+4}}{2}\)
Ta thấy x1 > x2 nên cần tìm m để x1 \(\ge\)2
Ta có : \(\frac{-m+\sqrt{m^2+4}}{2}\ge2\) \(\Leftrightarrow\sqrt{m^2+4}\ge m+4\)( 1 )
Nếu \(m\le-4\)thì ( 1 ) có VT > 0, VP < 0 nên ( 1 ) đúng
Nếu m > -4 thì ( 1 ) \(\Leftrightarrow m^2+4\ge m^2+8m+16\Leftrightarrow m\le\frac{-3}{2}\)
Ta được : \(-4< m\le\frac{-3}{2}\)
Tóm lại, giá trị phải tìm của m là \(m\le\frac{-3}{2}\)
CM
30 tháng 6 2017
Gọi x 0 là một nghiệm của phương trình x 2 - m x + 2 = 0
Suy ra 3 – x0 là một nghiệm của phương trình x 2 + 2 x - m = 0 .
Khi đó, ta có hệ
x 0 2 − m x 0 + 2 = 0 ( 3 − x 0 ) 2 + 2 ( 3 − x 0 ) − m = 0 ⇔ x 0 2 − m x 0 + 2 = 0 ( 1 ) m = x 0 2 − 8 x 0 + 15 ( 2 )
Thay (2) vào (1), ta được: x 0 2 − ( x 0 2 − 8 x 0 + 15 ) x 0 + 2 = 0 ⇔ x 0 = 2 x 0 = 7 ± 3 5 2 cho ta 3 giá trị của m cần tìm.
Đáp án cần chọn là: D
CM
16 tháng 8 2017
Gọi x0 là nghiệm chung của hai phương trình
thì x0 phải thỏa mãn hai phương trình trên:
Thay x = x0 vào hai phương trình trên ta được
x 0 2 + m x 0 + 1 = 0 x 0 2 + x 0 + m = 0
⇒ (m – 1)x0 + 1 – m = 0
⇔ (m – 1)(x0 – 1) = 0 (*)
Xét phương trình (*)
Nếu m = 1 thì 0 = 0 (luôn đúng)
hay hai phương trình trùng nhau
Lúc này phương trình x2 + x + 1 = 0
vô nghiệm nên cả hai phương trình đều vô nghiệm.
Vậy m = 1 không thỏa mãn.
+) Nếu m ≠ 1 thì x0 = 1
Thay x0 = 1 vào phương trình x02 + mx0 + 1 = 0 ta được m = −2
Thay m = −2 thì hai phương trình có nghiệm chung
Đáp án cần chọn là: D
2
28 tháng 5 2022
Ptr có:`\Delta=(-m)^2-4(m-3)=m^2-4m+12=(m-2)^2+8 > 0 AA m`
`=>` Ptr luôn có nghiệm `AA m`
`=>` Áp dụng Viét có:`{(x_1+x_2=[-b]/a=m),(x_1.x_2=c/a=m-3):}`
Ta có:`A=2(x_1 ^2+x_2 ^2)-x_1.x_2`
`<=>A=2[(x_1+x_2)^2-2x_1.x_2]-x_1.x_2`
`<=>A=2[m^2-2(m-3)]-(m-3)`
`<=>A=2(m^2-2m+6)-m+3`
`<=>A=2m^2-4m+12-m+3=2m^2-5m+15`
`<=>A=2(m^2-5/2+15/2)`
`<=>A=2[(m-5/4)^2+95/16]`
`<=>A=2(m-5/4)^2+95/8`
Vì `2(m-5/4)^2 >= 0 AA m<=>2(m-5/4)^2+95/8 >= 95/8 AA m`
Hay `A >= 95/8 AA m`
Dấu "`=`" xảy ra`<=>(m-5/4)^2=0<=>m=5/4`
Vậy `GTN N` của `A` là `95/8` khi `m=5/4`
AD
6 tháng 6 2023
\(\Delta=\left(-m\right)^2-2.1.\left(m-1\right)\\ =m^2-2m+1\\ =\left(m-1\right)^2\)
Phương trình có hai nghiệm phân biệt :
\(\Leftrightarrow\Delta>0\\ \Rightarrow\left(m-1\right)^2>0\\ \Rightarrow m\ne1\)
Theo vi ét :
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-1\end{matrix}\right.\)
\(x^2_1+x^2_2=x_1+x_2\\ \Leftrightarrow x^2_1+x^2_2=m\\ \Leftrightarrow\left(x^2_1+2x_1x_2+x_2^2\right)-2x_1x_2=m\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2-m=0\\ \Leftrightarrow m^2-2\left(m-1\right)-m=0\\ \Leftrightarrow m^2-2m+2-m=0\\ \Leftrightarrow m^2-3m+2=0\\ \Leftrightarrow\left[{}\begin{matrix}m=1\left(loại\right)\\m=2\left(t/m\right)\end{matrix}\right.\)
Vậy \(m=2\)
CM
22 tháng 11 2017
Đáp án C
Giả sử hai phương trình đã cho có nghiệm phức chung z 0 khi đó ta có hệ phương trình:
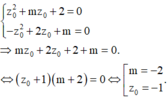
TH1: Nếu m = -2 thì khi đó 2 phương trình trở thành: z 2 − 2 z + 2 = 0 trùng nhau nên có nghiệm chung.
TH2: Nếu z 0 = − 1 thay vào hệ ta được:
1 − m + 2 = 0 − 1 − 2 + m = 0 ⇔ m = 3 .
Vậy giá trị cần tìm là m = -2 và m = 3.
DT
19 tháng 4 2023
Với phương trình: \(x^2+mx+n=0\)
delta 1 = \(m^2-4n\) (1)
Với phương trình: \(x^2-2x-n=0\)
delta 2 = \(\left(-2\right)^2-4.\left(-n\right)=4+4n\) (2)
Lấy (1) + (2) được \(m^2+4>0\forall m,n\)
=> delta 1 hoặc 2 luôn có ít nhất một delta không âm hay:
Với mọi giá trị của m và n thì ít nhất một trong hai phương trình trên có nghiệm.
☕T.Lam