b) #Toán lớp 8
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 8 2017
a) (2x+12x−1−2x−12x+1):4x10x−5=(2x+1)2−(2x−1)2(2x−1)(2x+1).10x+54x(2x+12x−1−2x−12x+1):4x10x−5=(2x+1)2−(2x−1)2(2x−1)(2x+1).10x+54x
=4x2+4x+1−4x2+4x−1(2x−1)(2x+1).5(2x+1)4x4x2+4x+1−4x2+4x−1(2x−1)(2x+1).5(2x+1)4x
=8x.5(2x+1)(2x−1)(2x+1).4x=102x−18x.5(2x+1)(2x−1)(2x+1).4x=102x−1
b) (1x2+x−2−xx+1):(1x+x−2)(1x2+x−2−xx+1):(1x+x−2)
=(1x(x+1)+x−2x+1):1+x2−2xx(1x(x+1)+x−2x+1):1+x2−2xx
=1+x(x−2)x(x+1).xx2−2x+11+x(x−2)x(x+1).xx2−2x+1
=(x2−2x+1)xx(x+1)(x2−2x+1)=1x+1(x2−2x+1)xx(x+1)(x2−2x+1)=1x+1
c) 1x−1−x3−xx2+1.(1x2−2x+1+11−x2)1x−1−x3−xx2+1.(1x2−2x+1+11−x2)
=1x−1−x3−xx2+1.[1(x−1)2−1(x−1)(x+1)]
TN
1 tháng 8 2017
a) (2x+12x−1−2x−12x+1):4x10x−5(2x+12x−1−2x−12x+1):4x10x−5
= 0 - 0
= 0
b) (1x2+x−2−xx+1):(1x+x−2);(1x2+x−2−xx+1):(1x+x−2)
= (x-xx+1) : (2x-2) : (x-xx+1) : (2x-2)
c) 1x−1−x3−xx2+1.(1x2−2x+1+11−x2)
= -2x-1-xx2+1. (14 - 4x)
= -x2-1-xx2+14-4x
= -6x-xx2+13
CM
8 tháng 3 2017
Biểu thức xác định khi x – 1 ≠ 0, x 2 - 2 x + 1 ≠ 0 và x 2 - 1 ≠ 0
x – 1 ≠ 0 ⇒ x ≠ 1
x 2 - 2 x + 1 ≠ 0 ⇒ x - 1 2 ≠ 0 ⇒ x ≠ 1
x 2 - 1 ≠ 0 ⇒ (x – 1)(x + 1) ≠ 0 ⇒ x ≠ -1 và x ≠ 1
Vậy biểu thức xác định với x ≠ -1 và x ≠ 1
Ta có:
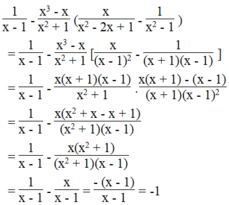
Vậy biểu thức không phụ thuộc vào biến x.
CM
28 tháng 9 2017
a) Tìm được x = 2,2
b) Tìm được x = 2073
c) Tìm được x = 4 hoặc x = -2
d) Điều kiện x≠-1 . Tìm được x = 0 hoặc x = 3
CM
13 tháng 3 2019
a) (x – 1)(x2 + x + 1) – 2x = x(x – 1)(x + 1)
⇔ x3 – 1 – 2x = x(x2 – 1)
⇔ x2 – 1 – 2x = x3 – x
⇔ -2x + x = 1 ⇔ - x = 1 ⇔ x = -1
Tập nghiệm của phương trình: S = { -1}
b) x2 – 3x – 4 = 0
⇔ x2 – 4x + x – 4 = 0 ⇔ x(x – 4) + (x – 4) = 0
⇔ (x – 4)(x + 1) = 0 ⇔ x – 4 = 0 hoặc x + 1 = 0
⇔ x = 4 hoặc x = -1
Tập nghiệm của phương trình: S = {4; -1}
c) ĐKXĐ : x – 1 ≠ 0 và x2 + x + 1 ≠ 0 (khi đó : x3 – 1 = (x – 1)(x2 + x + 1) ≠ 0)
⇔ x ≠ 1
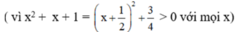
Quy đồng mẫu thức hai vế:
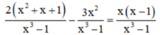
Khử mẫu, ta được: 2x2 + 2x + 2 – 3x2 = x2 – x
⇔ -2x2 + 3x + 2 = 0 ⇔ 2x2 – 3x – 2 = 0
⇔ 2x2 – 4x + x – 2 = 0 ⇔ 2x(x – 2) + (x – 2) = 0
⇔ (x – 2)(2x + 1) = 0 ⇔ x – 2 = 0 hoặc 2x + 1 = 0
⇔ x = 2 hoặc x = -1/2(thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {2 ; -1/2}
d) ĐKXĐ : x – 5 ≠ 0 và x – 1 ≠ 0 (khi đó : x2 – 6x + 5 = (x – 5)(x – 1) ≠ 0)
Quy đồng mẫu thức hai vế :
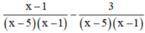
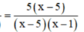
Khử mẫu, ta được : x – 1 – 3 = 5x – 25 ⇔ -4x = -21
⇔ x = 21/4 (thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {21/4}
RG
0
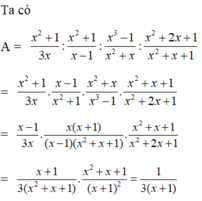
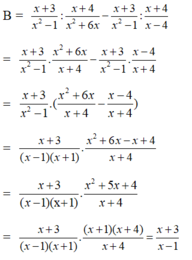
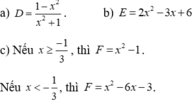
Hình như bạn hơi rảnh thì phải...
sorry minh gui sai cau hoi