Cho các số thực x, y thoả mãn x2+y2=5 Tìm Giá Trị Lớn Nhất Của Biểu Thức P= x+2y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
30 tháng 6 2023
Lời giải:
$A=(x+y)(x^2-xy+y^2)+x^2+y^2=2(x^2-xy+y^2)+x^2+y^2=2(x^2+y^2)+(x-y)^2$
$\geq 2(x^2+y^2)=(1^2+1^2)(x^2+y^2)\geq (x+y)^2=2^2=4$ (theo BĐT Bunhiacopxky)
Vậy $A_{\min}=4$. Giá trị này đạt tại $x=y=1$
TV
1
NM
Nguyễn Minh Quang
Giáo viên
2 tháng 9 2021
ta có
\(A^2=\left(x+2y\right)^2\le\left(1^2+2^2\right)\left(x^2+y^2\right)=25\left(\text{ BĐT Bunhia}\right)\)
vậy ta có \(A\le5\)hay GTLN của A là 5
V
1
DH
18 tháng 4 2021
Áp dụng BĐT cói cho 2 số ko âm ta có
X^2+y^2 >= 2 .căn x^2 .y^2 = 2.xy= 2.6 =12
Vậy P min =12 dấu = xảy ra khi x^2=y^2 <=> x=y
( thông cảm mình gõ mũ ko đc )
KN
31 tháng 1 2020
Bạn tham khảo nhé!
Câu hỏi của Lê VĂn Chượng - Toán lớp 10 - Học toán với OnlineMath
B1
1
PN
2 tháng 9 2020
Ta có : \(x^2+y^2=4< =>x^2+y^2\ge\frac{\left(x+y\right)^2}{2}\)
\(< =>4\ge\frac{\left(x+y\right)^2}{2}< =>\left(x+y\right)^2\le4.2=8< =>x+y\le\sqrt{8}\)
Hay \(x+y\le\sqrt{8}\)
Dấu = xảy ra khi và chỉ khi \(x=y=\sqrt{2}\)
Vậy GTLN của P = \(\sqrt{8}\)đạt được khi và chỉ khi \(x=y=\sqrt{2}\)
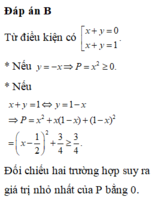
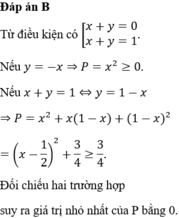
\(P-\dfrac{5}{2}=x+2y-\dfrac{x^2+y^2}{2}=-\dfrac{1}{2}\left(x-1\right)^2-\dfrac{1}{2}\left(y-2\right)^2+\dfrac{5}{2}\le\dfrac{5}{2}\)
\(\Rightarrow P-\dfrac{5}{2}\le\dfrac{5}{2}\Rightarrow P\le5\)
\(P_{max}=5\) khi \(\left(x;y\right)=\left(1;2\right)\)
Cảm ơn nhiều ạ !