Cho hình thoi ABCD, gọi O là giao điểm của 2 đường chéo AC và BD. Qua B vẽ đường thẳng song song với AC. Qua C vẽ đường thẳng song song với BD, chúng cắt nhau tại I
a. Chứng minh OBIC là hình chữ nhật
b.Chứng minh AB=OI
c. Tìm điều kiện của hình thoi ABCD để tứ giác OBIC là hình vuông

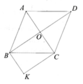
Hình vẽ và giả thiết tụ vẽ nhé+)
a) Có ABCD là hình thoi
⇒ BD ⊥ AC tại O ⇒ \(\widehat{BOC}\)= 90o
Có: BK ⊥ AC (gt)
BD ⊥ AC
=> BD ⊥ BK => \(\widehat{DBK} \) = 90o
Có: KC // BD (gt)
BD ⊥ AC
=> KC ⊥ AC => \(\widehat{OCK}\) = 90o
Xét tứ giác OBKC có:
\(\widehat{BOK} = \widehat{OBK} = \widehat{OCK} = 90\)o
=> tứ giác OBKC là hình chữ nhật
b) có tứ giác OBKC là hình chữ nhật ( ý a )
=> OK = BC
mà BC = AB ( tính chất hình thoi )
=> AB = OK
c) Để được OBKC là hình vuông
<=> OB = OC ( 2 cạnh kề nhau )
OB = \(\frac{1}{2}\) BD
OC = \(\frac{1}{2}\) AC
=> AC = BD
=> ABCD là hình vuông
Vậy hình thoi ABCD là hình vuông thì OBKC là hình vuông